题目内容
13.已知直线l:5x+12y=60,则直线上的点与原点的距离的最小值等于$\frac{60}{13}$.分析 直线上的点与原点的距离的最小值为原点到直线的距离.
解答 解:直线上的点与原点的距离的最小值为原点到直线的距离d=$\frac{|0+0-60|}{\sqrt{{5}^{2}+1{2}^{2}}}$=$\frac{60}{13}$.
故答案为:$\frac{60}{13}$.
点评 本题考查了点到直线的距离公式、圆的标准方程,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.从长方体一个顶点出发的三条棱长分别为2、3、4,则其对角线的长为( )
| A. | 3 | B. | 5 | C. | $\sqrt{26}$ | D. | $\sqrt{29}$ |
18.计算log232•log327=(( )
| A. | 12 | B. | 10 | C. | 15 | D. | 18 |
3.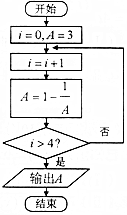 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )
 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 3 |