题目内容
【题目】德国著名数学家狄利克雷(Dirichlet,1805~1859)在数学领域成就显著.19世纪,狄利克雷定义了一个“奇怪的函数” 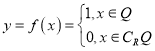 其中R为实数集,Q为有理数集.则关于函数
其中R为实数集,Q为有理数集.则关于函数![]() 有如下四个命题,正确的为( )
有如下四个命题,正确的为( )
A.函数![]() 是偶函数
是偶函数
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一个不为零的有理数T,![]() 对任意的
对任意的![]() 恒成立
恒成立
D.不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
【答案】ACD
【解析】
根据函数的定义以及解析式,逐项判断即可.
对于A,若![]() ,则
,则![]() ,满足
,满足![]() ;若
;若![]() ,则
,则![]() ,满足
,满足![]() ;故函数
;故函数![]() 为偶函数,选项A正确;
为偶函数,选项A正确;
对于B,取![]() ,则
,则![]() ,
,![]() ,故选项B错误;
,故选项B错误;
对于C,若![]() ,则
,则![]() ,满足
,满足![]() ;若
;若![]() ,则
,则![]() ,满足
,满足![]() ,故选项C正确;
,故选项C正确;
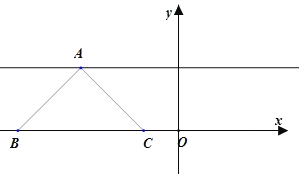
对于D,要为等腰直角三角形,只可能如下四种情况:
①直角顶点![]() 在
在![]() 上,斜边在
上,斜边在![]() 轴上,此时点
轴上,此时点![]() ,点
,点![]() 的横坐标为无理数,则
的横坐标为无理数,则![]() 中点的横坐标仍然为无理数,那么点
中点的横坐标仍然为无理数,那么点![]() 的横坐标也为无理数,这与点
的横坐标也为无理数,这与点![]() 的纵坐标为1矛盾,故不成立;
的纵坐标为1矛盾,故不成立;
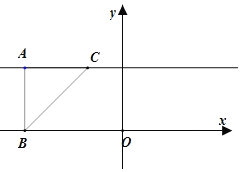
②直角顶点![]() 在
在![]() 上,斜边不在
上,斜边不在![]() 轴上,此时点
轴上,此时点![]() 的横坐标为无理数,则点
的横坐标为无理数,则点![]() 的横坐标也应为无理数,这与点
的横坐标也应为无理数,这与点![]() 的纵坐标为1矛盾,故不成立;
的纵坐标为1矛盾,故不成立;
③直角顶点![]() 在
在![]() 轴上,斜边在
轴上,斜边在![]() 上,此时点
上,此时点![]() ,点
,点![]() 的横坐标为有理数,则
的横坐标为有理数,则![]() 中点的横坐标仍然为有理数,那么点
中点的横坐标仍然为有理数,那么点![]() 的横坐标也应为有理数,这与点
的横坐标也应为有理数,这与点![]() 的纵坐标为0矛盾,故不成立;
的纵坐标为0矛盾,故不成立;
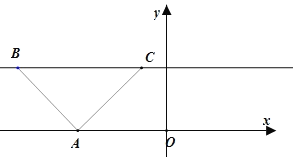
④直角顶点![]() 在
在![]() 轴上,斜边不在
轴上,斜边不在![]() 上,此时点
上,此时点![]() 的横坐标为无理数,则点
的横坐标为无理数,则点![]() 的横坐标也应为无理数,这与点
的横坐标也应为无理数,这与点![]() 的纵坐标为1矛盾,故不成立.
的纵坐标为1矛盾,故不成立.

综上,不存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等腰直角三角形,故选项D正确.
为等腰直角三角形,故选项D正确.
故选:![]() .
.

【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: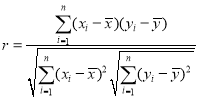 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |