题目内容
在直角坐标系xOy中,以O为极点,x正半轴为极轴建立极坐标系曲线C的极坐标方程为cos(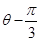 )=1,M,N分别为C与x轴,y轴的交点。
)=1,M,N分别为C与x轴,y轴的交点。
(I)写出C的直角坐标方程,并求M,N的极坐标;
(II)设MN的中点为P,求直线OP的极坐标方程。
(I)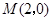 ,
,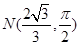 (II)
(II)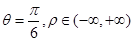
解析试题分析:(Ⅰ)由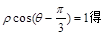
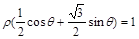 ,从而C的直角坐标方程为
,从而C的直角坐标方程为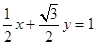 ,即
,即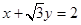 ,
,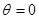 时,
时,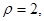 所以
所以 时,
时,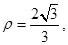 所以
所以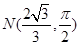
(Ⅱ)M点的直角坐标为(2,0),N点的直角坐标为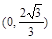 ,所以P点的直角坐标为
,所以P点的直角坐标为 所以直线OP的极坐标方程为
所以直线OP的极坐标方程为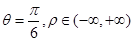 .
.
考点:点的极坐标和直角坐标的互化;简单曲线的极坐标方程.
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 的左右焦点坐标分别是
的左右焦点坐标分别是 ,离心率
,离心率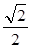 ,直线
,直线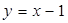 与椭圆
与椭圆 .
. 的长度.
的长度.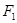 ,
,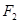 分别是椭圆
分别是椭圆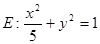 的左、右焦点
的左、右焦点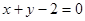 的对称点是圆
的对称点是圆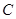 的一条直径的两个端点。
的一条直径的两个端点。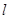 被椭圆
被椭圆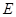 和圆
和圆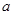 ,
,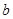 。当
。当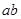 最大时,求直线
最大时,求直线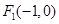 及
及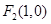 ,点
,点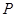 在以
在以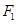 、
、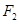 为焦点的椭圆
为焦点的椭圆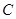 上,且
上,且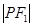 、
、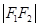 、
、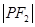 构成等差数列.
构成等差数列.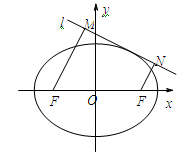
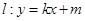 与椭圆
与椭圆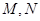 是直线上的两点,且
是直线上的两点,且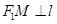 ,
,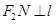 . 求四边形
. 求四边形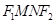 面积
面积 的最大值.
的最大值. :
: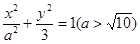 的右焦点
的右焦点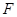 在圆
在圆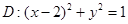 上,直线
上,直线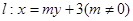 交椭圆于
交椭圆于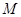 、
、 两点.
两点.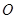 为坐标原点),求
为坐标原点),求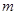 的值;
的值; 设点
设点 轴的对称点为
轴的对称点为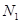 (
( ,试问
,试问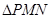 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由. 的左、右焦点分别是
的左、右焦点分别是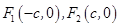 ,Q是椭圆外的动点,满足
,Q是椭圆外的动点,满足 .点
.点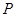 是线段
是线段 与该椭圆的交点,点T是
与该椭圆的交点,点T是 的中点.
的中点.
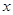 为点
为点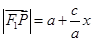 ;
; 的方程.
的方程. 过椭圆
过椭圆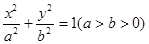 的两焦点,与椭圆有且仅有两个公共点:直线
的两焦点,与椭圆有且仅有两个公共点:直线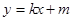 与圆
与圆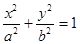 相交于A,B两点记
相交于A,B两点记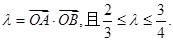
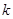 的取值范围;
的取值范围;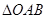 的面积S的取值范围.
的面积S的取值范围. 的对称轴为坐标轴,焦点是(0,
的对称轴为坐标轴,焦点是(0,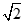 ),(0,
),(0,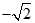 ),又点
),又点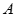
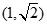 在椭圆
在椭圆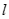 的斜率为
的斜率为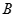 、
、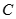 两点,求
两点,求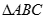 面积的最大值.
面积的最大值.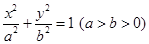 过点
过点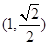 ,离心率为
,离心率为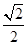 ,左、右焦点分别为
,左、右焦点分别为 、
、 .点
.点 为直线
为直线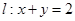 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线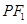 和
和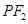 与椭圆的交点分别为
与椭圆的交点分别为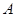 、
、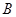 和
和 、
、 ,
,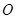 为坐标原点.设直线
为坐标原点.设直线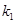 、
、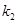 .
.
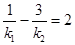 ;
; 上是否存在点
上是否存在点 、
、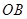 、
、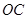 、
、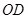 的斜率
的斜率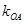 、
、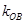 、
、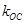 、
、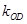 满足
满足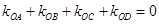 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点