题目内容
已知椭圆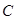 的左右焦点坐标分别是
的左右焦点坐标分别是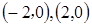 ,离心率
,离心率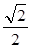 ,直线
,直线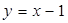 与椭圆
与椭圆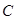 交于不同的两点
交于不同的两点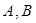 .
.
(1)求椭圆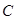 的方程;
的方程;
(2)求弦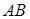 的长度.
的长度.
(1) 。(2)
。(2) 。
。
解析试题分析:
思路分析:(1)利用“待定系数法”设椭圆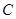 的方程为
的方程为 由
由 ,进一步确定b。
,进一步确定b。
(2)建立方程组 ,消去
,消去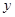 ,并整理得,应用韦达定理及弦长公式。
,并整理得,应用韦达定理及弦长公式。
解:(1)依题意可设椭圆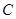 的方程为
的方程为 1分
1分
则 ,解得
,解得 3分
3分 5分
5分 椭圆
椭圆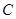 的方程为
的方程为 6分
6分
(2)设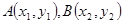 7分
7分
联立方程 ,消去
,消去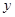 ,
,
并整理得: 9分
9分 10分
10分
 12分
12分
即 13分
13分
考点:椭圆的标准方程,直线与椭圆的位置关系。
点评:中档题,确定椭圆的标准方程,一般利用“待定系数法”,由a,b,c,e的关系,建立方程组。涉及直线与椭圆的位置关系,往往通过联立方程组,应用韦达定理,简化解题过程。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
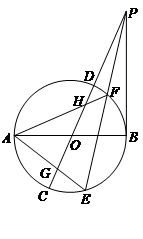
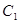 ,求证:O、
,求证:O、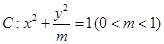 的左顶点为
的左顶点为 ,
,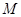 是椭圆
是椭圆 上异于点
上异于点 与点
与点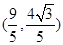 ,求
,求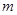 的值;
的值;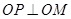 ,求
,求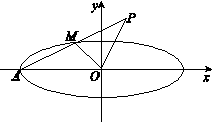
 的圆心为
的圆心为 ,动圆
,动圆 过点
过点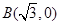 ,且和圆
,且和圆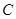 .
.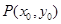 为曲线
为曲线 与曲线
与曲线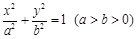 ,其离心率为
,其离心率为 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3. 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足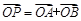 ,求
,求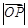 的取值范围.
的取值范围.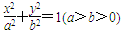 的离心率e为
的离心率e为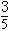 , 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
, 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合. -6x+1与坐标轴的交点都在圆C上.
-6x+1与坐标轴的交点都在圆C上.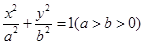 右焦点的直线
右焦点的直线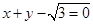 交
交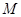 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为 .
.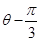 )=1,M,N分别为C与x轴,y轴的交点。
)=1,M,N分别为C与x轴,y轴的交点。