题目内容

20．从A、B、C、D、E等5名短跑运动员中，任选4名排在标号分别为1、2、3、4的跑道上，求运动员E排在1、2跑道上的概率．

分析 先求出从A、B、C、D、E等5名短跑运动员中，任选4名排在标号分别为1、2、3、4的跑道上的基本事件总数，再求出运动员E排在1、2跑道上，包含的基本事件个数，由此能求出运动员E排在1、2跑道上的概率．

解答 解：从A、B、C、D、E等5名短跑运动员中，任选4名排在标号分别为1、2、3、4的跑道上，
基本事件总数n=${C}_{5}^{4}$=120，
运动员E排在1、2跑道上，包含的基本事件个数m=${C}_{2}^{1}{A}_{4}^{3}$=48，
∴运动员E排在1、2跑道上的概率p=$\frac{m}{n}=\frac{48}{120}$=$\frac{2}{5}$．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件率计算公式的合理运用．

练习册系列答案
相关题目
10．若sinα=$\frac{\sqrt{2}}{4}$，α∈（0，$\frac{π}{2}$），则sin（α+$\frac{π}{4}$）=$\frac{1+\sqrt{7}}{4}$．
11．“x1＞3且x2＞3”是“x1+x2＞6且x1x2＞9”的充要条件吗？若是，请说明理由；若不是，请给出“x1＞3且x2＞3”的充要条件．
8．已知f（x）=x2-a|x-1|-1，a∈R．
（1）当a=0时，判断函数f（x）的奇偶性，并用定义证明；
（2）若f（x）≥0对x∈[1，+∞）恒成立，求a的取值范围；
（3）写出f（x）在[-2，2]上的最大值g（a）．（不需要解答过程）
15．已知圆C：x2+y2+2x-4y+m=0与y轴相切．
（1）求m的值；
（1）若圆C的切线在x轴和y轴上的截距相等，求该切线的方程；
（2）从圆C外一点P（x，y）向圆引切线，M为切点，O为坐标原点，且有|PM|=|PO|，求使|PM|最小的点P的坐标．
5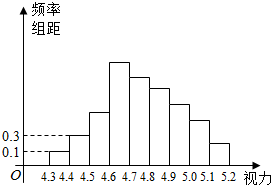．为了解某校学生的视力情况，随机抽查了该校的100名学生，得到如图所示的频率分布直方图，由于不慎将部分数据丢失，但知道前4组的频数和为40，后6组的频数和为87，设最大频率a视力在4.5到5.2之间的学生数b，则a，b的值分别为（　　）
A．0.27，96B．0.27，83C．2.7，78D．2.7，83
12．已知偶函数f（x）=ln|x|，则满足f（2x-1）＜f（$\frac{1}{3}$）的取值范围是（　　）
A．（$\frac{2}{3}$，1）B．（$\frac{1}{2}$，$\frac{2}{3}$）C．（0，$\frac{2}{3}$）D．（-∞，$\frac{2}{3}$）
9．在△ABC中，已知向量$\overrightarrow{a}$=（2sinB，1），$\overrightarrow{b}$=（cosA，sin（A+C）），若$\overrightarrow{a}$⊥$\overrightarrow{b}$．
（I）求角A；
（Ⅱ）若BC=$\sqrt{21}$，△ABC的面积是$\sqrt{3}$，若AB＜AC，求AB．
15．若$\overrightarrow{a}$=（2+λ，1），$\overrightarrow{b}$=（3，λ），若＜$\overrightarrow{a}$，$\overrightarrow{b}$＞为钝角，则实数λ的取值范围是$λ＜-\frac{3}{2}$且λ≠-3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网