题目内容
18.已知偶函数f(x)的导数为f′(x)(x∈R),且在[0,+∞)上满足f′(x)<x3,若f(m-3)-f(m)≥$\frac{1}{4}$[(m-3)4-m4],则实数m的取值范围为[$\frac{3}{2}$,+∞).分析 构造辅助函数g(x)=f(x)-$\frac{1}{4}{x}^{4}$,由题意可得g(x)是偶函数,求导判断g(x)的单调性,把f(m-3)-f(m)≥$\frac{1}{4}$[(m-3)4-m4]转化为g(m-3)≥g(m),利用单调性转化为关于m的不等式求解.
解答 解:令g(x)=f(x)-$\frac{1}{4}{x}^{4}$,
∵g(-x)-g(x)=f(-x)-$\frac{1}{4}(-x)^{4}$-f(x)-$\frac{1}{4}{x}^{4}$=0,
∴函数g(x)为偶函数,
∵x∈[0,+∞)时,g′(x)=f′(x)-x3<0,
∴函数g(x)在x∈[0,+∞)为减函数,
f(m-3)-f(m)≥$\frac{1}{4}$[(m-3)4-m4],即f(m-3)-$\frac{1}{4}(m-3)^{4}$≥f(m)-$\frac{1}{4}{m}^{4}$,
也即g(m-3)≥g(m),
∴g(|m-3|)≥g(|m|),
则|m-3|≤|m|,解得:m$≥\frac{3}{2}$.
∴实数m的取值范围为[$\frac{3}{2}$,+∞).
故答案为:[$\frac{3}{2}$,+∞).
点评 本题考查利用导数研究函数的单调性,考查数学转化思想方法,正确构造函数是关键,是中档题.

练习册系列答案
相关题目
8.已知平面α和两条直线a,b,则下列结论成立的是( )
| A. | 如果a∥α,b∥α,那么a∥b | |
| B. | 如果a∥b,a∥α,b?α,那么b∥α | |
| C. | 如果a∥b,那么α平行于经过b的任何平面 | |
| D. | 如果a∥α,那么a与α内的任何直线平行 |
13.函数f(x)=x2-8lnx的单调递减区间为( )
| A. | [2,+∞) | B. | (-∞,2] | C. | (0,2] | D. | (-2,2) |
3.把红、蓝、白3张纸牌随机地分发给甲、乙、丙三个人,每人分得1张,事件“甲分得红牌”与事件“乙分得红牌”是( )
| A. | 对立事件 | B. | 不可能事件 | ||
| C. | 互斥但不对立事件 | D. | 以上都不对 |
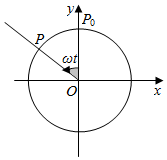 如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).
如图,点P是半径为1的砂轮边缘上的一个质点,它从初始位置P0开始,按逆时针方向以角速度ω=1rad/s做圆周运动,记点P的纵坐标y关于时间t(t≥0,t的单位:s)的函数关系为y=f(t).