题目内容
某工厂生产某种儿童玩具,每件玩具的成本价为30元,并且每件玩具的加工费为t元(其中t为常数,且2≤t≤5),设该工厂每件玩具的出厂价为x元(35≤x≤41),根据市场调查,日销售量与ex(e为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
(1)求该工厂的日利润y(元)与每件玩具的出厂价x元的函数关系式;
(2)当每件玩具的日售价为多少元时,该工厂的利润y最大,并求y的最大值.
(1)设日销售量为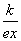 ,则
,则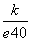 =10,∴k=10e40,
=10,∴k=10e40,
则日销售量为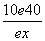 件,∴日利润y=(x-30-t)·
件,∴日利润y=(x-30-t)·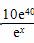 .
.
∴y=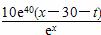 (35≤x≤41).
(35≤x≤41).
(2)y′=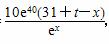 ,令y′=0得x=31+t.
,令y′=0得x=31+t.
①当2≤t≤4时,33≤31+t≤35,
∴当35≤x≤41时,y′≤0.
∴当x=35时,y取最大值,最大值为10(5-t)e5.
②当4<t≤5时,35<t+31≤36,函数y在[35,t+31]上单调递增,在[t+31,41]上单调递减.
∴当x=t+31时,y取最大值10e9-t.
∴当2≤t≤4,x=35时,日利润最大值为10(5-t)e5元;
当4<t≤5,x=31+t时,日利润最大值为10e9-t元.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 ,n∈N+,则数列{an}的前n项和是( )
,n∈N+,则数列{an}的前n项和是( )
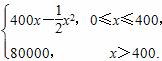 则总利润最大时,每年生产的产品产量是( )
则总利润最大时,每年生产的产品产量是( ) (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.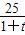 (t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )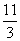
 4xdx,则公比q的值为( )
4xdx,则公比q的值为( )
 的弦被点(4,2)平分,则这条弦所在的直线方程是( )
的弦被点(4,2)平分,则这条弦所在的直线方程是( ) (B)
(B) (C)
(C) (D)
(D)