Question

求曲线f(x)＝x3－3x2＋2x过原点的切线方程．

Answer 1

解　f′(x)＝3x2－6x＋2，设切线的斜率为k.

(1)当切点是原点时k＝f′(0)＝2，f(0)＝0，

所以所求曲线的切线方程为y＝2x.

(2)当切点不是原点时，设切点是(x0，y0)，

则有y0＝x－3x＋2x0，k＝f′(x0)＝3x－6x0＋2，①

又k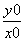＝＝x－3x0＋2，                      ②

由①②得x0＝，k＝＝－.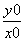

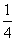∴所求曲线的切线方程为y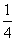＝－x.