题目内容
若集合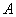 具有以下性质:①
具有以下性质:①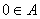 ,
,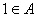 ;②若
;②若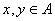 ,则
,则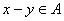 ,且
,且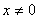 时,
时,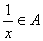 .
.
则称集合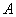 是“好集”.(Ⅰ)分别判断集合
是“好集”.(Ⅰ)分别判断集合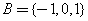 ,有理数集
,有理数集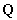 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(Ⅱ)设集合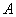 是“好集”,求证:若
是“好集”,求证:若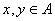 ,则
,则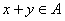 ;(Ⅲ)对任意的一个“好集”
;(Ⅲ)对任意的一个“好集”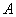 ,
, 分别判断下面命题的真假,并说明理由.命题
分别判断下面命题的真假,并说明理由.命题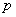 :若
:若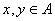 ,则必有
,则必有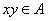 ;命题
;命题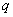 :若
:若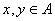 ,且
,且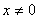 ,则必有
,则必有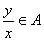 ;
;
解:(Ⅰ)集合 不是“好集”. 理由是:假设集合
不是“好集”. 理由是:假设集合 是“好集”. 因为
是“好集”. 因为 ,
, ,所以
,所以 . 这与
. 这与 矛盾. 有理数集
矛盾. 有理数集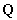 是“好集”. 因为
是“好集”. 因为 ,
, ,对任意的
,对任意的 ,有
,有 ,且
,且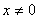 时,
时, .
.
所以有理数集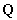 是“好集”.
是“好集”.
(Ⅱ)因为集合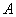 是“好集”,所以
是“好集”,所以 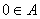 .若
.若 ,则
,则 ,即
,即 .所以
.所以 ,即
,即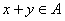 .
.
(Ⅲ)命题 均为真命题. 理由如下: 对任意一个“好集”
均为真命题. 理由如下: 对任意一个“好集”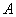 ,任取
,任取 ,
,
若 中有0或1时,显然
中有0或1时,显然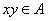 .下设
.下设 均不为
均不为 0,1
0,1 . 由定义可知:
. 由定义可知: .
.
所以  ,即
,即 .所以
.所以  . 由(Ⅱ)可得:
. 由(Ⅱ)可得: ,即
,即 . 同理可得
. 同理可得 .若
.若 或
或 ,则显然
,则显然 .若
.若 且
且 ,则
,则 .
.
所以  .所以
.所以  由(Ⅱ)可得:
由(Ⅱ)可得: .所以
.所以 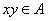 .
.
综上可知,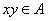 ,即命题
,即命题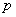 为真命题.若
为真命题.若 ,且
,且 ,则
,则 .所
.所 以
以  ,即命题
,即命题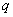 为真命题.
为真命题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,且
,且 没有实数根,那么
没有实数根,那么 的实根根数个数为()
的实根根数个数为()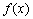 的定义域为
的定义域为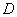 ,若
,若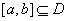 ,使
,使 上的值域为
上的值域为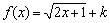 为闭函数,那么
为闭函数,那么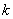 的取值范围是
的取值范围是 ≤
≤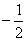 B.
B. 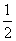 ≤
≤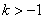 D.
D. 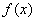 ,当
,当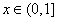 时,
时,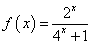 .
.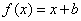 在[-1,1]上恒有实数解,求实数b的取值范围.
在[-1,1]上恒有实数解,求实数b的取值范围. =
= 当2<a<3<b<4时,函数
当2<a<3<b<4时,函数 .
.  ,已知函数
,已知函数 的定义域是
的定义域是 ,值域是
,值域是 ,若函数g(x)=2︱x-1︱+m+1有唯一的零点,则
,若函数g(x)=2︱x-1︱+m+1有唯一的零点,则 ( )A.2 B.
( )A.2 B.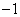 C.1 D.0
C.1 D.0 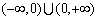 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列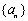 ,
, 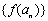 仍是等比数列,则称
仍是等比数列,则称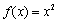 ; ②
; ②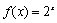 ; ③
; ③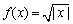 ; ④
; ④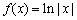 .则其中是“保等比数列函数”的
.则其中是“保等比数列函数”的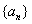 满足
满足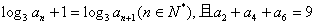 ,则
,则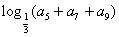 的值是
的值是 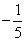 C.
C.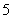 D.
D.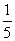
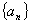 中,若
中,若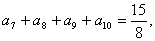
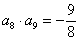 ,则
,则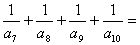 。
。