题目内容
已知函数f(x)=
(1)求f(2)与f(
),f(3)与f(
)的值;
(2)由(1)中求得的结果,你能发现f(x)与f(
)有什么关系?证明你的发现;
(3)求下列式子的值.f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(
)+f(
)+…+f(
)+f(
)
| x2 |
| 1+x2 |
(1)求f(2)与f(
| 1 |
| 2 |
| 1 |
| 3 |
(2)由(1)中求得的结果,你能发现f(x)与f(
| 1 |
| x |
(3)求下列式子的值.f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
考点:归纳推理,函数的值
专题:计算题,推理和证明
分析:(1)利用f(x)=
,代入计算,求f(2)与f(
),f(3)与f(
)的值;
(2)f(x)+f(
)=1,利用f(x)=
,即可证明;
(3)利用f(x)+f(
)=1,可得结论.
| x2 |
| 1+x2 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)f(x)+f(
| 1 |
| x |
| x2 |
| 1+x2 |
(3)利用f(x)+f(
| 1 |
| x |
解答:
解:(1)f(2)=
,f(
)=
,f(3)=
,f(
)=
;
(2)f(x)+f(
)=1,证明如下:
f(x)+f(
)=
+
=1;
(3)f(0)=0,f(1)=
,
∴f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(
)+f(
)+…+f(
)+f(
)=0+
+2013=2013
.
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 9 |
| 10 |
| 1 |
| 3 |
| 1 |
| 10 |
(2)f(x)+f(
| 1 |
| x |
f(x)+f(
| 1 |
| x |
| x2 |
| 1+x2 |
| ||
1+
|
(3)f(0)=0,f(1)=
| 1 |
| 2 |
∴f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2013 |
| 1 |
| 2014 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查归纳推理,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若数列{an}是等差数列,a3,a10是方程x2-3x-5=0的两根,则a5+a8=( )
| A、4 | B、2 | C、-3 | D、3 |
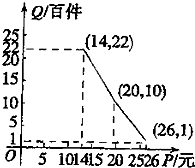 在对口扶贫活动中,企业甲将经营状况良好的某种消费品专卖店以优惠价格转让给小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3600元后,逐步偿还转让费(不计息).根据甲提供的资料有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2000元.
在对口扶贫活动中,企业甲将经营状况良好的某种消费品专卖店以优惠价格转让给小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3600元后,逐步偿还转让费(不计息).根据甲提供的资料有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2000元.