题目内容
4．在△ABC中，内角A，B，C的对边分别为a，b，c，且满足$\frac{cosB}{cosC}$+$\frac{2a}{c}+\frac{b}{c}$=0，则角C的大小为$\frac{2π}{3}$．分析 由三角函数公式和三角形的内角和以及正弦定理可得cosC，可得角C．
解答 解：∵在△ABC中$\frac{cosB}{cosC}$+$\frac{2a}{c}+\frac{b}{c}$=0，
∴由正弦定理可得$\frac{cosB}{cosC}$+$\frac{2sinA+sinB}{sinC}$=0，
∴cosBsinC+2sinAcosC+sinBcosC=0，
即sin（B+C）=-2sinAcosC，
故sinA=-2sinAcosC，
约掉sinA可得cosC=-$\frac{1}{2}$，
由三角形内角范围可得角C=$\frac{2π}{3}$
故答案为：$\frac{2π}{3}$．
点评 本题考查正弦定理解三角形，涉及三角函数公式的应用，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．设函数f（x）对x≠0的实数满足f（x）-2f（$\frac{1}{x}$）=3x+2，那么${∫}_{1}^{2}$f（x）dx=（ ）
| A． | -（$\frac{7}{2}$+2ln2） | B． | $\frac{7}{2}$+2ln2 | C． | -（$\frac{7}{2}$+ln2） | D． | -（4+2ln2） |
12．
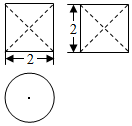如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图，则该几何体的体积为（ ）
如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图，则该几何体的体积为（ ）| A． | $\frac{1}{3}$π | B． | $\frac{2}{3}$π | C． | $\frac{4}{3}$π | D． | $\frac{5}{3}$π |
14．下列命题为真命题的是（ ）
| A． | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| B． | 若p∨q为真命题，则p∧q为真命题 | |
| C． | 命题“x＜-1，则x2-2x-3＞0”的否命题为“若x＜-1，则x2-2x-3≤0” | |
| D． | 若命题p：?x∈R，使x2+x+1＜0，则￢p：?x∈R，使x2+x+1≥0 |