题目内容
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<1,则
的取值范围是 .
(
,5)解析:观察图象,可知f(x)在(-∞,0]上是减函数,在[0,+∞)上是增函数,
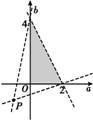
由f(2a+b)<1=f(4),可得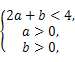
画出以(a,b)为坐标的可行域(如图阴影部分所示),
而可看成(a,b)与点P(-1,-1)连线的斜率,可求得(,5)为所求.
练习册系列答案
相关题目
)处的切线与坐标轴围成的三角形面积为( )
(B)
(C)
= . 
x3+
x2+2ax.
,+∞)上存在单调递增区间,求a的取值范围;
,求f(x)在该区间上的最大值.
(单位:m/s).