题目内容
15.在平面直角坐标系中,曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{5}cosa}\\{y=sinα}\end{array}\right.$(α为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+$\frac{π}{4}$)=$\sqrt{2}$.l与C交于A、B两点.(Ⅰ)求曲线C的普通方程及直线l的直角坐标方程;
(Ⅱ)设点P(0,-2),求|PA|+|PB|的值.
分析 (Ⅰ)利用三种方程互化方法,曲线C的普通方程及直线l的直角坐标方程;
(Ⅱ)点P(0,-2)在l上,l的参数方程为为$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=-2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),代入$\frac{1}{5}$x2+y2=1整理得,3t2-10$\sqrt{2}$t+15=0,即可求|PA|+|PB|的值.
解答 解:(Ⅰ)曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{5}cosa}\\{y=sinα}\end{array}\right.$(α为参数),普通方程为C:$\frac{1}{5}$x2+y2=1;
直线l的极坐标方程为ρcos(θ+$\frac{π}{4}$)=$\sqrt{2}$,即ρcosθ-ρsinθ=2,l:y=x-2. …(4分)
(Ⅱ)点P(0,-2)在l上,l的参数方程为$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t}\\{y=-2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数)
代入$\frac{1}{5}$x2+y2=1整理得,3t2-10$\sqrt{2}$t+15=0,
由题意可得|PA|+|PB|=|t1|+|t2|=|t1+t2|=$\frac{10}{3}$$\sqrt{2}$ …(10分)
点评 本题考查三种方程互化,考查参数的几何意义,考查学生的计算能力,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
6.如图是某几何体的三视图,则该几何体的体积为( )
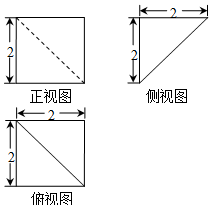

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
3.已知椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,F为椭圆C的右焦点,圆x2+y2=4上有一动点P,P不同于A,B两点,直线PA与椭圆C交于点Q,则$\frac{{k}_{PB}}{{k}_{QF}}$的取值范围是( )
| A. | (-∞,-$\frac{3}{4}$)∪(0,$\frac{3}{4}$) | B. | (-∞,0)∪(0,$\frac{3}{4}$) | C. | (-∞,-1)∪(0,1) | D. | (-∞,0)∪(0,1) |
7.为了调查黄山市某校高中学生是否愿意在寒假期间参加志愿者活动,用简单随机抽样方法从该校调查了80人,结果如下:
(1)若用分层抽样的方法在愿意参加志愿者活动的学生抽取5人,则应女生中抽取多少人?
(2)在(1)中抽取出的5人中任选2人,求“被选中的恰好是一男一女”的概率.
注:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 30 | 10 |
| 女生 | 20 | 20 |
(2)在(1)中抽取出的5人中任选2人,求“被选中的恰好是一男一女”的概率.
| P(K2≥k0) | 0.025 | 0.010 |
| k0 | 5.024 | 6.635 |