题目内容
3.已知椭圆C:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1的左、右顶点分别为A,B,F为椭圆C的右焦点,圆x2+y2=4上有一动点P,P不同于A,B两点,直线PA与椭圆C交于点Q,则$\frac{{k}_{PB}}{{k}_{QF}}$的取值范围是( )| A. | (-∞,-$\frac{3}{4}$)∪(0,$\frac{3}{4}$) | B. | (-∞,0)∪(0,$\frac{3}{4}$) | C. | (-∞,-1)∪(0,1) | D. | (-∞,0)∪(0,1) |
分析 取特殊点P(0,2),P(0,-2),求出$\frac{{k}_{PB}}{{k}_{QF}}$,利用排除法,可得结论.
解答 解:取特殊点P(0,2),则PA方程为y=x+2
与椭圆方程联立,可得7x2+16x+4=0=0,所以x=-2或-$\frac{2}{7}$,所以Q(-$\frac{2}{7}$,$\frac{12}{7}$),
∴kPB=-1,kQF=$\frac{\frac{12}{7}}{-\frac{2}{7}-1}$=-$\frac{3}{4}$,
∴$\frac{{k}_{PB}}{{k}_{QF}}$=$\frac{3}{4}$.
同理取P(0,-2),$\frac{{k}_{PB}}{{k}_{QF}}$=-$\frac{3}{4}$.
根据选项,排除A,B,C,
故选D.
点评 本题考查圆与圆锥曲线的综合,考查特殊法的运用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知全集U={1,2,3,4,5,6,7},集合A={1,3,7},B={x|x=log2(a+1),a∈A},则(∁UA)∩(
(∁UB)=( )
(∁UB)=( )
| A. | {1,3} | B. | {5,6} | C. | {4,5,6} | D. | {4,5,6,7} |
8.不等式2x2-x-3>0解集为( )
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
12.已知数列 {an} 的前 n 项和为Sn,S1=6,S2=4,Sn>0且S2n,S2n-1,S2n+2成等比数列,S2n-1,S2n+2,S2n+1成等差数列,则a2016等于( )
| A. | -1009 | B. | -1008 | C. | -1007 | D. | -1006 |
 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.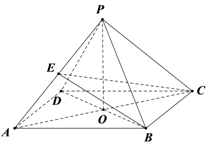 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O