题目内容
6.如图是某几何体的三视图,则该几何体的体积为( )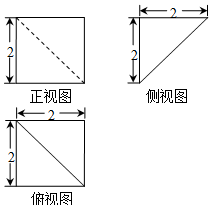
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
分析 几何体为不规则放置的四棱锥,做出棱锥的直观图,利用作差法求出棱锥的体积即可.
解答 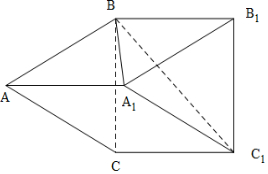 解:由三视图可知几何体为直三棱柱切去一个三棱锥得到的四棱锥,直观图如图所示:
解:由三视图可知几何体为直三棱柱切去一个三棱锥得到的四棱锥,直观图如图所示:
其中直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=BC=2,AB⊥BC,
直三棱柱的高AA1=2,
∴四棱锥B-ACC1A1的体积V=V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{B-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}×2×2×2$-$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{8}{3}$.
故选A.
点评 本题考查了空间几何体的三视图,空间几何体的体积计算,属于中档题.

练习册系列答案
相关题目
18.已知全集U={1,2,3,4,5,6,7},集合A={1,3,7},B={x|x=log2(a+1),a∈A},则(∁UA)∩(
(∁UB)=( )
(∁UB)=( )
| A. | {1,3} | B. | {5,6} | C. | {4,5,6} | D. | {4,5,6,7} |
 四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )
四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )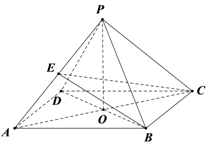 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O