题目内容
19.在长方体ABCD-A1B1C1D1中,AB=1,BC=3,AA1=2,E,F分别是下底面的棱A1B1,B1C1的中点,M是上底面的棱AD上一点,且AM=2,过M,E,F的平面与BA的延长线交于点N,则MN的长度为( )| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{10}}}{3}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{{2\sqrt{10}}}{3}$ |
分析 如图连结AC,作MH∥AC交CD与H,得EF∥AC∥MH,过M,E,F的平面与面ABCD的交线时MH,延长HM交BA延长线与N,根据相似可求MN.
解答 解:如图连结AC,作MH∥AC交CD与H,∵E,F分别是棱A1B1,B1C1的中点,∴EF∥AC∥MH,
过M,E,F的平面与面ABCD的交线时MH,延长HM交BA延长线与N,
根据AN∥HD可得$\frac{HM}{MN}=\frac{MD}{MA}=\frac{1}{2}$,∴$MN=\frac{2}{3}HN=\frac{2}{3}AC=\frac{2}{3}×\sqrt{10}$,∴MN的长度为$\frac{2\sqrt{10}}{3}$,
故选:D,
:

点评 本题考查了空间作图,即线段的长度求解,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
9.有下列命题:(1)若z是复数,则|z|2=z2;(2)任意两个复数不能比较大小;(3)b2-4ac>0时,一元二次方程ax2+bx+c=0(a,b,c∈C)有两个不等的实数根,其中所有错误命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
10.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则该三棱锥S-ABC的外接球的表面积为( )
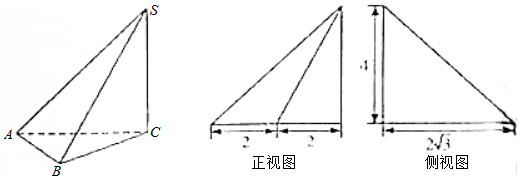

| A. | 32π | B. | $\frac{112π}{3}$ | C. | $\frac{28π}{3}$ | D. | $\frac{64}{3}$π |
7.已知函数f(x)=sin(2x+$\frac{π}{12}$),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
| A. | [$\frac{π}{12}$,$\frac{7π}{12}$] | B. | [-$\frac{5π}{12}$,$\frac{π}{12}$] | C. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | D. | [-$\frac{π}{6}$,$\frac{5π}{6}$] |
14.已知集合A={x|x2-6x+5≤0},B={x|y=log2(x-2)},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (2,5] | D. | [2,5] |
8.执行如图所示的程序框图,若输出结果是5,则输入的整数p的可能性有( )


| A. | 6种 | B. | 7种 | C. | 8种 | D. | 9种 |
9.复数z=$\frac{(i-1)^{2}+1}{{i}^{2}}$的实部为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |