题目内容
8.为了得到函数y=sin(2x-$\frac{π}{3}$)的图象,只需把函数y=cos(2x-$\frac{4π}{3}$)的图象( )| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
分析 利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:把函数y=cos(2x-$\frac{4π}{3}$)=sin(2x-$\frac{5π}{6}$)的图象向左平移$\frac{π}{4}$个单位长度,
可得y=sin[2(x+$\frac{π}{4}$)-$\frac{5π}{6}$]=sin(2x-$\frac{π}{3}$)的图象,
故选:A.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知命题p:|x-4|≤6,q:x2-m2-2x+1≤0(m>0),若¬p是¬q的必要不充分条件,则实数m的取值范围为( )
| A. | [9,13] | B. | (3,9) | C. | [9,+∞) | D. | (9,+∞) |
13.设x,y满足约束条件$\left\{\begin{array}{l}y-x≤0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$,则z=x-3y的最大值为( )
| A. | 4 | B. | $\frac{3}{2}$ | C. | $-\frac{8}{3}$ | D. | 2 |
20.若函数f(x)=aex-x-2a有两个零点,则实数a的取值范围是( )
| A. | $({-∞,\frac{1}{e}})$ | B. | $({0,\frac{1}{e}})$ | C. | (-∞,0) | D. | (0,+∞) |
17.下列说法正确的是( )
| A. | 若$\frac{1}{a}>\frac{1}{b}$,则a<b | |
| B. | 若命题$P:?x∈({0,π}),x+\frac{1}{sinx}≤2$,则?P为真命题 | |
| C. | 已知命题p,q,“p为真命题”是“p∧q为真命题”的充要条件 | |
| D. | 若f(x)为R上的偶函数,则$\int_{-1}^1{f(x)dx}=0$ |
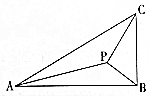 如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.