题目内容
已知函数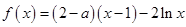 ,
,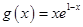 (
( ,
,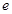 为自然对数的底数).
为自然对数的底数).
(1)当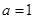 时,求
时,求 的单调区间;
的单调区间;
(2)对任意的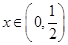 ,
,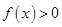 恒成立,求
恒成立,求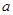 的最小值;
的最小值;
(3)若对任意给定的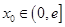 ,在
,在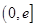 上总存在两个不同的
上总存在两个不同的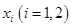 ,使得
,使得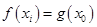 成立,求
成立,求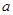 的取值范围.
的取值范围.
(1)函数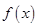 的单调减区间为
的单调减区间为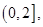 单调增区间为
单调增区间为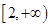 ;(2)实数
;(2)实数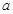 的最小值为
的最小值为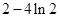 ;
;
(3)实数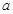 的取值范围是
的取值范围是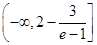 .
.
解析试题分析:(1)把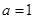 代入函数
代入函数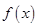 的解析式,直接利用导数求函数
的解析式,直接利用导数求函数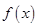 在定义域上的单调区间;(2)利用参数分离法将问题中的不等式等价转化为
在定义域上的单调区间;(2)利用参数分离法将问题中的不等式等价转化为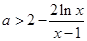 在
在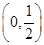 上恒成立,即
上恒成立,即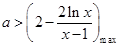 ,进而求出参数
,进而求出参数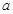 的取值范围,从而求出
的取值范围,从而求出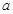 的最小值;(3)先利用导数求出函数
的最小值;(3)先利用导数求出函数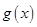 在
在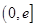 上的值域,利用导数研究函数
上的值域,利用导数研究函数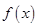 的单调性,并求出方程
的单调性,并求出方程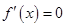 的唯一根
的唯一根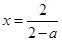 ,将条件“对于任意给定的
,将条件“对于任意给定的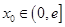 ,在
,在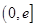 总存在两个不同的
总存在两个不同的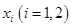 ,使得
,使得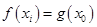 ”转化为“函数
”转化为“函数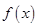 在区间
在区间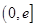 上存在唯一极值点
上存在唯一极值点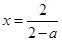 ,即
,即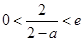 ,且函数
,且函数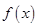 在区间
在区间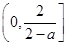 和区间
和区间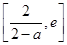 上的值域均包含函数
上的值域均包含函数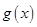 在区间
在区间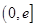 上的值域”,从而列出相应的不等式进行求解参数
上的值域”,从而列出相应的不等式进行求解参数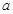 的取值范围.
的取值范围.
试题解析:(1)当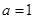 时,
时,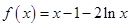 ,
,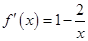 ,
,
由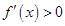 ,
,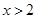 ,由
,由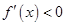 ,
,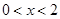 ,
,
故 的单调减区间为
的单调减区间为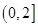 ,单调增区间为
,单调增区间为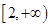 ;
;
(2)即对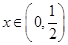 ,
,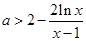 恒成立,
恒成立,
令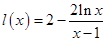 ,
,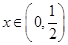 ,则
,则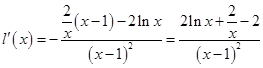 ,
,
再令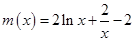 ,
,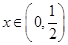 ,
,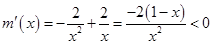 ,
,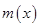 在
在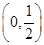 上为减函数,于是
上为减函数,于是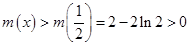 ,
,
从而,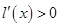 ,于是
,于是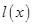 在
在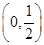 上为增函数,
上为增函数,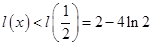 ,
,
故要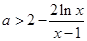 恒成立,只要
恒成立,只要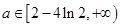 ,即
,即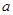 的最小值为
的最小值为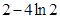 ;
;
(3)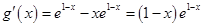 ,当
,当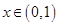 时,
时,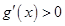 ,函数
,函数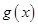 单调递增,
单调递增,
当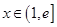 时,
时,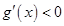 ,函数
,函数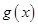 单调递减,
单调递减,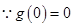 ,
,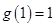 ,
,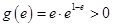 ,
,
所以,函数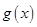 在
在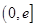 上的值域为
上的值域为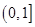 .
.
当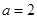 时,不合题意;
时,不合题意;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
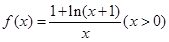
 在区间
在区间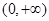 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;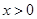 时,
时,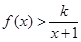 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;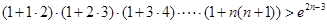
 排水管,在路南侧沿直线
排水管,在路南侧沿直线 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为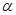 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.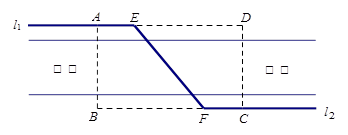
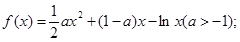
 的单调区间;
的单调区间; 使
使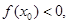 求实数a的范围.
求实数a的范围.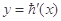 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)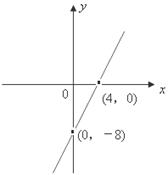
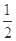 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;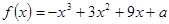 .
. 的单调递减区间;
的单调递减区间;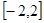 上的最大值为
上的最大值为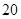 ,求它在该区间上的最小值.
,求它在该区间上的最小值.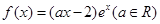 的一个极值点,
的一个极值点,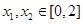 时,证明:
时,证明: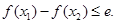
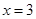 是函数
是函数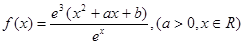 的一个极值点.
的一个极值点.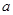 与
与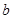 的关系式(用
的关系式(用 的单调递增区间;
的单调递增区间;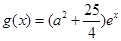 ,若存在
,若存在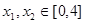 使得
使得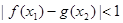 成立,求实数
成立,求实数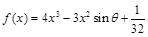 ,其中
,其中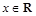 ,
,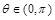 .
.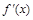 的最小值为
的最小值为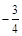 ,试判断函数
,试判断函数 的零点个数,并说明理由;
的零点个数,并说明理由;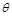 的取值范围.
的取值范围.