题目内容
10.已知函数f(x)=|x|+$\frac{m}{x}$-1(x≠0).(1)当m=5时,判断f(x)在(-∞,0)的单调性,并用定义证明;
(2)若对任意x∈R,不等式f(2x)>0恒成立,求m的取值范围;
(3)讨论f(x)零点的个数.
分析 (1)当m=5时,且x<0时,$f(x)=-x+\frac{5}{x}-1$是单调递减的.利用核对单调性的定义,设x1<x2<0,判断f(x1)-f(x2)>0,推出结果,
(2)由f(2x)>0得$|{2^x}|+\frac{m}{2^x}-1>0$,变形为(2x)2-2x+m>0,即m>2x-(2x)2,利用二次函数的最值求解即可.
(3)由f(x)=0可得x|x|-x+m=0(x≠0),变为m=-x|x|+x(x≠0),令$g(x)=x-x|x|=\left\{{\begin{array}{l}{-{x^2}+x,x>0}\\{{x^2}+x,x<0}\end{array}}\right.$,作y=g(x)的图象及直线y=m,求解零点个数.
解答 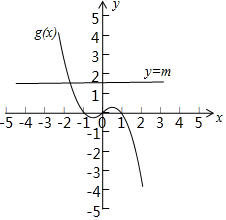 解:(1)当m=5时,且x<0时,$f(x)=-x+\frac{5}{x}-1$是单调递减的.
解:(1)当m=5时,且x<0时,$f(x)=-x+\frac{5}{x}-1$是单调递减的.
证明:设x1<x2<0,则$f({x_1})-f({x_2})=(-{x_1}+\frac{5}{x_1}-1)-(-{x_2}+\frac{5}{x_2}-1)$=$({x_2}-{x_1})+(\frac{5}{x_1}-\frac{5}{x_2})=({x_2}-{x_1})+\frac{{5({x_2}-{x_1})}}{{{x_1}{x_2}}}=({x_2}-{x_1})(1+\frac{5}{{{x_1}{x_2}}})$,
又x1<x2<0,所以x2-x1>0,x1x2>0,所以$({x_2}-{x_1})(1+\frac{5}{{{x_1}{x_2}}})>0$,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
故当m=5时,$f(x)=-x+\frac{5}{x}-1$在(-∞,0)上是单调递减的.
(2)由f(2x)>0得$|{2^x}|+\frac{m}{2^x}-1>0$,变形为(2x)2-2x+m>0,即m>2x-(2x)2,
而${2^x}-{({2^x})^2}=-{({2^x}-\frac{1}{2})^2}+\frac{1}{4}$,
当${2^x}=\frac{1}{2}$即x=-1时${({2^x}-{({2^x})^2})_{max}}=\frac{1}{4}$,所以$m>\frac{1}{4}$.
(3)由f(x)=0可得x|x|-x+m=0(x≠0),变为m=-x|x|+x(x≠0),
令$g(x)=x-x|x|=\left\{{\begin{array}{l}{-{x^2}+x,x>0}\\{{x^2}+x,x<0}\end{array}}\right.$,
作y=g(x)的图象及直线y=m,由图象可得:
当$m>\frac{1}{4}$或$m<-\frac{1}{4}$时,f(x)有1个零点.
当$m=\frac{1}{4}$或m=0或$m=-\frac{1}{4}$时,f(x)有2个零点.
当$0<m<\frac{1}{4}$或$-\frac{1}{4}<m<0$时,f(x)有3个零点.
点评 本题考查函数与方程的综合应用,函数的图象,零点个数,函数恒成立,考查转化思想以及计算能力.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\sqrt{2}$ |
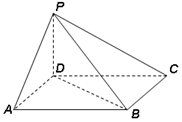 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD. 如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.