题目内容
15.如果一个水平放置的图形的斜二测直观图是一个腰为1的等腰直角三角形,那么原平面图形的面积是( )| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\sqrt{2}$ |
分析 根据图形的斜二测直观图是等腰直角三角形,它的底角为45°,两腰长均为1,求出直观图的面积,利用原图和直观图的面积关系得到答案.
解答 解:∵图形的斜二测直观图是一个等腰直角三角形,它的底角为45°,两腰长均为1,
∴直观图的面积S=$\frac{1}{2}$,
则原图的面积S′=2$\sqrt{2}$S=$\sqrt{2}$,
故选:D.
点评 本题考查的知识点是空间几何体的直观图,熟练掌握原图面积S′和直观图的面积S的关系S′=2$\sqrt{2}$S是解答的关键.

练习册系列答案
相关题目
6.下列四个函数中是R上的减函数的为( )
| A. | $y={log_2}{2^{-x}}$ | B. | $y={({\frac{1}{2}})^{-x}}$ | C. | $y=\frac{1}{x+1}$ | D. | y=x2 |
7.已知点(1,-2)在抛物线y=ax2的准线上,则a的值为( )
| A. | $\frac{1}{8}$ | B. | -$\frac{1}{8}$ | C. | 8 | D. | -8 |
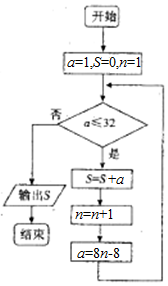 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )