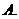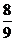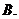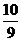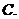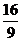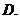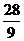题目内容
如图所示:一块椭圆形状的铁板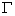 的长轴长为4米,短轴长为2米.
的长轴长为4米,短轴长为2米.
 (1)若利用这块椭圆铁板
(1)若利用这块椭圆铁板 截取矩形,要求矩形的
截取矩形,要求矩形的
四个顶点都在椭圆铁板 的边缘,求所能截取
的边缘,求所能截取
的矩形面积的最大值;
(2)若以短轴的端点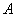 为直角顶点,另外两个锐
为直角顶点,另外两个锐
角的顶点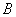 、
、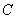 都在椭圆铁板的边缘,切割
都在椭圆铁板的边缘,切割
等腰直角三角形,则在不同的切割方案中,
共能切割出几个面积不同的等腰直角三角形?
最大面积是多少?(结果保留一位小数)
解:(1)建系(略),得椭圆的标准方程为 -设矩形的一个顶点坐标为
-设矩形的一个顶点坐标为
 -当且仅当
-当且仅当 ,即
,即 时等号成立.
时等号成立.
(2)设 所在的直线方程为:
所在的直线方程为: ,则
,则 所在的直线方程为:
所在的直线方程为: ---2分
---2分
将 所在的直线方程代入椭圆方程,得
所在的直线方程代入椭圆方程,得
可求得,
同理可求得 ,
,
不妨设 ,令
,令 ,得
,得 ,
,
即 ,
,
解得, 或
或 .
.
当 时,所截取等腰直角三角形面积为2.6平方米;
时,所截取等腰直角三角形面积为2.6平方米;
当 时,所截取等腰直角三角形面积为2.1平方米.
时,所截取等腰直角三角形面积为2.1平方米.
所以,切割出的等腰直角三角形的最大面积约2.6平方米.

练习册系列答案
相关题目
 与圆
与圆 相交于
相交于 ,
, 两点,若
两点,若 ,则实数
,则实数 的值
的值 的准线与直线
的准线与直线 之间的距离为3,则该抛物线的方程为 .
之间的距离为3,则该抛物线的方程为 . 则不等式
则不等式 的解集为_______.
的解集为_______. ,
, ,那么 【 】
,那么 【 】 真包含于
真包含于 B.
B.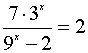 的解是 .
的解是 .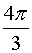 ,则圆锥的体积是________
,则圆锥的体积是________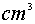 .
. 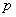 为假命题,命题
为假命题,命题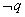 为假命题,则命题“
为假命题,则命题“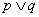 ”为假命题;
”为假命题;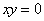 ,则
,则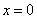 或
或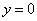 ”的否命题为“若
”的否命题为“若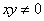 ,则
,则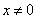 或
或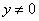 ”;
”;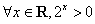 ”的否定是“
”的否定是“ 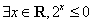 ”.则以上结论正确的个数为
”.则以上结论正确的个数为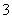 B.
B.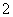 C.
C.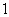 D.
D.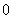
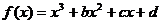 的大致图像,
的大致图像, 则
则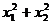 等于( )
等于( )