题目内容
若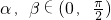
，且sinα-cosβ＜0，则
- A.α＜β
- B.α＞β
- C.
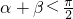
- D.
C
分析：题中条件：“sinα-cosβ＜0”转化为sinα＜cosβ，再化成同名三角函数，利用三角函数的单调性解决．
解答：∵sinα-cosβ＜0
∴sinα＜cosβ，
∴sinα＜sin（
-β），
∵正弦函数在（0，）是单调增函数，
∴α＜-β，
∴．
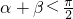故选C．
点评：本题主要考查三角函数的单调性，本题巧妙地运用了正弦函数的单调性，给出了简捷的证明，比较时应注意把两个函数值转化为同一单调区间上的同名函数．
分析：题中条件：“sinα-cosβ＜0”转化为sinα＜cosβ，再化成同名三角函数，利用三角函数的单调性解决．
解答：∵sinα-cosβ＜0
∴sinα＜cosβ，
∴sinα＜sin（
-β），∵正弦函数在（0，
）是单调增函数，∴α＜
-β，∴
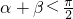．故选C．
点评：本题主要考查三角函数的单调性，本题巧妙地运用了正弦函数的单调性，给出了简捷的证明，比较时应注意把两个函数值转化为同一单调区间上的同名函数．
练习册系列答案
相关题目
若θ是△ABC的一个内角，且sinθcosθ=-
，则sinθ-cosθ的值为（ ）
| 1 |
| 8 |
A、-
| ||||
B、
| ||||
| C、tan2A+cot2A=7 | ||||
D、
|
若θ为三角形的一个内角，且sinθ+cosθ=
，则曲线x2sinθ+y2cosθ=1是（ ）
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
，且sinα-cosβ＜0，则（ ）
