题目内容
若θ为三角形的一个内角,且sinθ+cosθ=
,则曲线x2sinθ+y2cosθ=1是( )
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
分析:把sinθ+cosθ=
两边平方可得,sinθ•cosθ=-
<0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.
| 1 |
| 2 |
| 3 |
| 4 |
解答:解:因为θ∈(0,π),且sinθ+cosθ=
,所以θ∈(
,π),
且|sinθ|>|cosθ|,所以θ∈(
,
),从而cosθ<0,
从而x2sinθ+y2cosθ=1表示焦点在xy轴上的双曲线.
故选 C.
| 1 |
| 2 |
| π |
| 2 |
且|sinθ|>|cosθ|,所以θ∈(
| π |
| 2 |
| 3π |
| 4 |
从而x2sinθ+y2cosθ=1表示焦点在xy轴上的双曲线.
故选 C.
点评:本题考查椭圆的标准方程形式,由三角函数式判断角的取值范围.

练习册系列答案
相关题目
球面上有三点A、B、C组成球的一个内接三角形,若AB =18,BC
=24,AC =30,且球心到平面ABC的距离等于球的半径的一半,那么球面面积为( )
|
(A) |
(B) 300π |
(C) 1200π |
(D) 1600π |
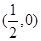 的距离比它到y轴的距离大
的距离比它到y轴的距离大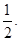
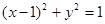 的外切三角形,求△QBC面积的最小值。
的外切三角形,求△QBC面积的最小值。