题目内容
若θ是△ABC的一个内角,且sinθcosθ=-
,则sinθ-cosθ的值为( )
| 1 |
| 8 |
A、-
| ||||
B、
| ||||
| C、tan2A+cot2A=7 | ||||
D、
|
分析:先根据题设条件判断出sinθ>0,cosθ<0,进而可知sinθ-cosθ>0,进而利用同角三角函数基本关系利用sinθ-cosθ=
求得答案.
| 1-2sinθcosθ |
解答:解:∵sinθcosθ=-
∴sinθ>0且cosθ<0
∴sinθ-cosθ>0,
∴sinθ-cosθ=
=
=
=
故选D
| 1 |
| 8 |
∴sinθ-cosθ>0,
∴sinθ-cosθ=
| (sinθ-cosθ)2 |
| 1-2sinθcosθ |
1+
|
| ||
| 2 |
故选D
点评:本题主要考查同角三角函数基本关系的运用.解题时要注意对三角函数值正负号的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若A是△ABC的一个内角,且sinA+cosA=
,△ABC的形状是( )
| 2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
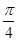 ,
,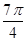 ]上的简图;
]上的简图;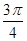 ]上的单调递增区间;试问:当x在R上取何值
]上的单调递增区间;试问:当x在R上取何值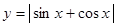
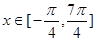 的简图;
的简图;