题目内容
若θ是△ABC的一个内角,且sinθcosθ=-
,则cosθ-sinθ的值为( )
| 1 |
| 8 |
分析:由θ为三角形的内角,且sinθcosθ=-
<0,判断得出cosθ-sinθ的正负,将所求式子平方利用同角三角函数间的基本关系及完全平方公式变形,开方即可求出值.
| 1 |
| 8 |
解答:解:∵θ为△ABC内角,且sinθcosθ=-
<0,
∴cosθ<0,sinθ>0,
即cosθ-sinθ<0,
∵(cosθ-sinθ)2=1-2sinθcosθ=1+
=
,
∴cosθ-sinθ=-
.
故选C
| 1 |
| 8 |
∴cosθ<0,sinθ>0,
即cosθ-sinθ<0,
∵(cosθ-sinθ)2=1-2sinθcosθ=1+
| 1 |
| 4 |
| 5 |
| 4 |
∴cosθ-sinθ=-
| ||
| 2 |
故选C
点评:此题考查了同角三角哦函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
若A是△ABC的一个内角,且sinA+cosA=
,△ABC的形状是( )
| 2 |
| 3 |
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
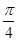 ,
,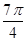 ]上的简图;
]上的简图;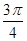 ]上的单调递增区间;试问:当x在R上取何值
]上的单调递增区间;试问:当x在R上取何值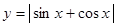
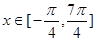 的简图;
的简图;