题目内容
已知椭圆 ,过点
,过点
 作直线
作直线 与椭圆交于
与椭圆交于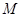 、
、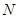 两点.
两点.
(1) 若点 平分线段
平分线段 ,试求直线
,试求直线 的方程;
的方程;
设与满足(1)中条件的直线 平行的直线与椭圆交于
平行的直线与椭圆交于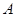 、
、 两点,
两点,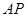 与椭圆交于点
与椭圆交于点 ,
, 与椭圆交于点
与椭圆交于点 ,求证:
,求证: //
//
 ,过点
,过点
 作直线
作直线 与椭圆交于
与椭圆交于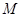 、
、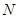 两点.
两点.(1) 若点
 平分线段
平分线段 ,试求直线
,试求直线 的方程;
的方程;设与满足(1)中条件的直线
 平行的直线与椭圆交于
平行的直线与椭圆交于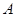 、
、 两点,
两点,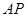 与椭圆交于点
与椭圆交于点 ,
, 与椭圆交于点
与椭圆交于点 ,求证:
,求证: //
//
(1) ,
, ,则有
,则有 ,
, .
.
 ①
①
 ②
②
① -②得 ,
,
即 , ………………4分
, ………………4分
得
故直线 的方程为
的方程为 ,
,
即 . ………………5分
. ………………5分
(2)证明:设 ,且
,且 .
.
则有 ,
, ,
,
即 . ………………6分
. ………………6分
将点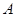 、
、 的坐标分别代入椭圆方程:
的坐标分别代入椭圆方程:
 ①
①
 ②
②
② -①得
-①得
 ………………8分
………………8分
易知 ,故约去
,故约去 得
得
 ③
③
同理有 ④
④
由④-③得 .
.
由已知, 斜率为
斜率为 ,有
,有 , ………………10分
, ………………10分
得
即 ,即
,即 ,
,
所以 //
// .
.
 ,
, ,则有
,则有 ,
, .
. ①
① ②
②① -②得
 ,
,即
 , ………………4分
, ………………4分得

故直线
 的方程为
的方程为 ,
,即
 . ………………5分
. ………………5分(2)证明:设
 ,且
,且 .
.则有
 ,
, ,
,即
 . ………………6分
. ………………6分将点
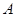 、
、 的坐标分别代入椭圆方程:
的坐标分别代入椭圆方程: ①
① ②
②②
 -①得
-①得 ………………8分
………………8分易知
 ,故约去
,故约去 得
得 ③
③同理有
 ④
④由④-③得
 .
.由已知,
 斜率为
斜率为 ,有
,有 , ………………10分
, ………………10分得

即
 ,即
,即 ,
,所以
 //
// .
. 略

练习册系列答案
相关题目
 点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,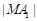 ∶
∶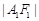 = 2∶1.
= 2∶1.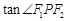 的最大值.
的最大值.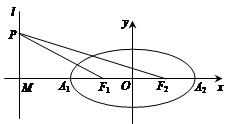
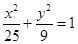 的左焦点为
的左焦点为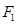 , 点
, 点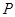 在椭圆上, 若线段
在椭圆上, 若线段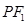 的中点
的中点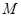 在
在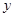 轴上, 则
轴上, 则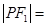


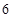
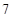
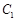 :
: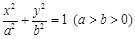 的离心率为
的离心率为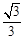 ,直线
,直线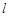 :
: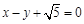 与椭圆
与椭圆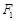 ,右焦点为
,右焦点为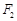 ,直线
,直线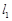 过点
过点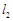 垂直于直线
垂直于直线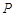 ,线段
,线段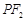 的垂直平分线交
的垂直平分线交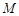 ,求点
,求点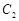 的方程.
的方程.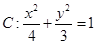 的左焦点
的左焦点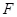 作倾斜角为
作倾斜角为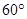 的直线
的直线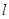 与椭圆
与椭圆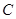 交于
交于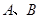 两点,则
两点,则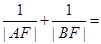 ( )
( )



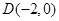 的直线
的直线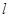 与椭圆
与椭圆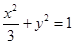 相交于不同的两点A、B,点M是弦AB的中点, 则
相交于不同的两点A、B,点M是弦AB的中点, 则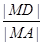 的最小值为 ( )
的最小值为 ( )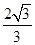 B.
B.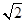 C. 1 D.
C. 1 D.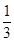
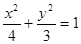 的焦距等于
的焦距等于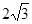
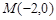 的直线
的直线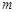 与椭圆
与椭圆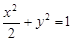 交于
交于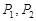 ,线段
,线段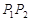 的中点为
的中点为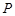 ,设直线
,设直线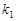 ,直线
,直线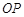 的斜率为
的斜率为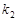 ,则
,则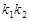 的值为
的值为 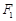 、
、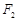 是椭圆C:
是椭圆C: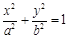 (
(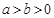 )的两个焦点,P为椭圆C上的一点,且
)的两个焦点,P为椭圆C上的一点,且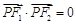 。若
。若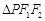 的面积为9,则
的面积为9,则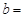 _________。
_________。