题目内容
14.直线3x+4y-8=0与直线3x+4y+7=0间的距离是3.分析 根据两条平行直线间的距离公式,求得直线3x+4y-8=0与直线3x+4y+7=0间的距离.
解答 解:根据两条平行直线间的距离公式可得,
直线3x+4y-8=0与直线3x+4y+7=0间的距离为$\frac{|-8-7|}{\sqrt{9+16}}$=3.
故答案为:3.
点评 本题主要考查两平行线间的距离公式的应用,要注意先把两直线的方程中x,y的系数化为相同的,然后才能用两平行线间的距离公式.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
5.已知f(x),g(x)定义在同一区间上,f(x)是增函数,g(x)是减函数,且g(x)≠0,则( )
| A. | f(x)+g(x) 为减函数 | B. | f(x)-g(x)为增函数 | C. | f(x)•g(x)是减函数 | D. | $\frac{f(x)}{g(x)}$ 是增函数 |
9.若不等式mx2+x+n>0的解集是{x|-$\frac{1}{3}$<x<$\frac{1}{2}$},则m,n分别是( )
| A. | 6,-1 | B. | -6,-1 | C. | 6,1 | D. | -6,1 |
3.若a>b>0,则下列不等式一定成立的是( )
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{b}{a}>\frac{b+1}{a+1}$ | C. | $a-\frac{1}{b}>b-\frac{1}{a}$ | D. | $\frac{2a+b}{a+2b}>\frac{a}{b}$ |
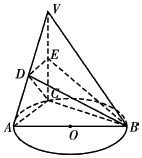 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.