题目内容
7.含有三个实数的集合既可表示成$\{a,\frac{b}{a},1\}$,又可表示成{a2,a+b,0},则a2017+b2016=-1.分析 利用集合相等求出a,b,然后求解表达式的值.
解答 解:有三个实数的集合,既可表示为$\{a,\frac{b}{a},1\}$,也可表示为{a2,a+b,0},
可得b=0,a=-1,则a2017+b2016=-1+0=-1,
故答案是:-1.
点评 本题考查集合相等,考查计算能力,是基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
17.已知函数$f(x)=\left\{\begin{array}{l}x+1(x<1)\\-x+3(x≥1)\end{array}\right.$,则$f[f(\frac{5}{2})]$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{2}$ |
16.在圆x2+y2=4上,与直线 l:4x+3y-12=0的距离最大的点的坐标是( )
| A. | $({\frac{8}{5},\frac{6}{5}})$ | B. | $({\frac{8}{5},-\frac{6}{5}})$ | C. | $({-\frac{8}{5},-\frac{6}{5}})$ | D. | $({-\frac{8}{5},\frac{6}{5}})$ |
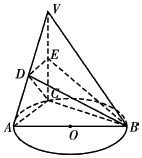 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.