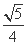题目内容
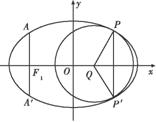
如图,椭圆的中心为原点O,长轴在x轴上,离心率e=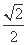 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点, 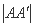 =4.
=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
解:(1)由题意知点A(-c,2)在椭圆上,则 +
+ =1,从而e2+
=1,从而e2+ =1,
=1,
又e=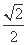 ,故b2=
,故b2= =8,从而a2=
=8,从而a2= =16.
=16.
故该椭圆的标准方程为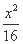 +
+ =1.
=1.
(2)由椭圆的对称性,可设Q(x0,0).又设M(x,y)是椭圆上任意一点,则|QM|2=(x-x0)2+y2=x2-2x0x+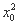 +8×(1-
+8×(1-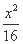 )=
)= (x-2x0)2-
(x-2x0)2-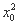 +8(x∈[-4,4]).
+8(x∈[-4,4]).
设P(x1,y1),由题意知,P是椭圆上到Q的距离最小的点,
因此,当x=x1时|QM|2取最小值,
又x1∈(-4,4),所以当x=2x0时|QM|2取最小值,
从而x1=2x0,且|QP|2=8-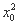 .
.
由对称性知P′(x1,-y1),故|PP′|=|2y1|,
所以S= |2y1||x1-x0|
|2y1||x1-x0|
= ×2
×2 |x0|
|x0|
=
= ·
· .
.
当x0=± 时,△PP′Q的面积S取得最大值2
时,△PP′Q的面积S取得最大值2 .
.
此时对应的圆Q的圆心坐标为Q(± ,0),半径|QP|=
,0),半径|QP|= =
= ,
,
因此,这样的圆有两个,其标准方程分别为(x+ )2+y2=6,(x-
)2+y2=6,(x- )2+y2=6.
)2+y2=6.

某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽20人调查对2016年巴黎奥运会筹备情况的了解,则应怎样抽样?
某河流上的一座水力发电站,每年六月份的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关.据统计,当X=70时,Y=460;X每增加10,Y增加5.已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:
近20年六月份降雨量频率分布表
| 降雨量 | 70 | 110 | 140 | 160 | 200 | 220 |
| 频率 |
|
|
|
|
|
|
(2)假定今年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
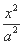 -
-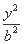 =1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且
=1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且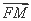 =2
=2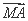 ,则双曲线C离心率是 .
,则双曲线C离心率是 . 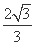 ).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点. +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.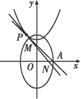
 (B)5 (C)
(B)5 (C)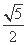 (D)
(D)
 ,则双曲线
,则双曲线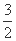 (D)
(D)