题目内容
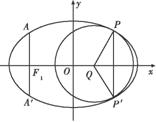
已知左焦点为F(-1,0)的椭圆过点E(1,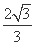 ).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
(1)求椭圆的标准方程;
(2)若P为线段AB的中点,求k1;
(3)若k1+k2=1,求证直线MN恒过定点,并求出定点坐标.
解:(1)依题设c=1,且右焦点F′(1,0).
所以2a=|EF|+|EF′|=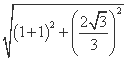 +
+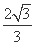
=2 ,
,
b2=a2-c2=2,
故所求的椭圆的标准方程为 +
+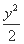 =1.
=1.
(2)设A(x1,y1),B(x2,y2),
则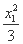 +
+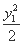 =1,①
=1,①
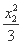 +
+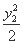 =1.②
=1.②
②-①,得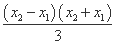 +
+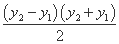 =0.
=0.
所以k1=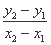 =-
=-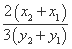 =-
=-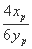 =-
=- .
.
(3)依题设,k1≠k2.
设M(xM,yM),
又直线AB的方程为y-1=k1(x-1),
即y=k1x+(1-k1),
亦即y=k1x+k2,
代入椭圆方程并化简得(2+3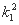 )x2+6k1k2x+3
)x2+6k1k2x+3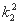 -6=0.
-6=0.
于是,xM=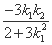 ,yM=
,yM=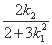 ,
,
同理,xN=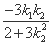 ,yN=
,yN= .
.
当k1k2≠0时,
直线MN的斜率k=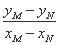 =
=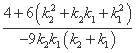
=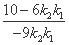 .
.
直线MN的方程为y-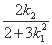 =
=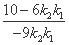 (x-
(x-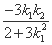 ),
),
即y=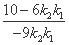 x+(
x+(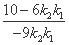 ·
·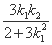 +
+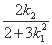 ),
),
亦即y=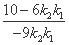 x-
x- .
.
此时直线过定点(0,- ).
).
当k1k2=0时,直线MN即为y轴,
此时亦过点(0,- ).
).
综上,直线MN恒过定点,且坐标为(0,- ).
).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
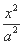 -
-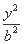 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( ) -
-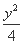 =1 (B)
=1 (B) 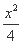 -
-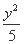 =1
=1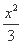 -
-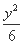 =1 (D)
=1 (D) 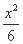 -
-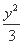 =1
=1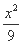 +
+ +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.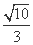 时,求k的值.
时,求k的值. x的焦点重合,则椭圆的方程为( )
x的焦点重合,则椭圆的方程为( ) +
+ =1 (B)
=1 (B)  =1
=1 =1 (D)
=1 (D)  +
+ =1
=1 )在椭圆C上,则椭圆C的标准方程为 .
)在椭圆C上,则椭圆C的标准方程为 .  -
- =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆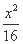 +
+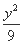 =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 . 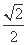 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点, 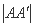 =4.
=4.