题目内容
已知圆C:x2+y2+6x+8y+21=0,抛物线y2=8x的准线为l,设抛物线上任意一点P到直线l的距离为m,则m+|PC|的最小值为 .
 解析:由题意得圆的方程为(x+3)2+(y+4)2=4,
解析:由题意得圆的方程为(x+3)2+(y+4)2=4,
圆心C的坐标为(-3,-4).
由抛物线定义知,当m+|PC|最小时为圆心与抛物线焦点间的距离,
即m+|PC|= =
= .
.

练习册系列答案
相关题目
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次,根据年龄将大众评委分为五组,各组的人数如下:
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
(1)为了调查评委对7位歌手的支持情况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取了6人,请将其余各组抽取的人数填入下表:
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 |
| 6 |
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
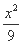 +
+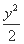 =1的焦点为F1、F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 .
=1的焦点为F1、F2,点P在椭圆上.若|PF1|=4,则|PF2|= ,∠F1PF2的大小为 .  -
- =1(a>0,b>0)和椭圆
=1(a>0,b>0)和椭圆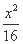 +
+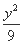 =1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
=1有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 . 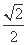 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点, 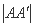 =4.
=4.