题目内容

函数f（x）=2sinxcosx+2cos2x，（x∈R）．
（1）求函数f（x）的最小正周期和对称中心坐标；
（2）若A为锐角三角形ABC的最大角，求f（A）的取值范围．
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（1）将函数进行化简，根据三角函数的图象和性质即可求函数f（x）的最小正周期和对称中心坐标；
（2）根据锐角三角形的性质，确定A的取值范围，即可得到结论．
解答： 解：（1）由条件，f（x）=2sinxcosx+2cos2x=sin2x+cos2x+1=
2
sin（2x+
π
4
）+1，
根据公式，最小正周期T=
2π
2
=π，
对称中心横坐标x应该满足2x+
π
4
=kπ，即x=
kπ
2
-
π
8
，k∈Z，此时y=1，
所以对称中心为（
kπ
2
-
π
8
，1）．
（2）因为A为锐角三角形ABC的最大角，所以A∈[
π
3
，
π
2
），
所以2A+
π
4
∈[
11π
12
，
5π
4
），由单调性，f（A）∈（0，
3
+1
2
]．
点评：本题主要考查三角函数的图象和性质，利用三角函数的关系式进行化简是解决本题的关键．
练习册系列答案
相关题目
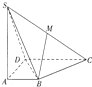四棱锥S-ABCD中，SA⊥平面ABCD，底面四边形ABCD为直角梯形，AB∥CD，AD⊥DC，SA=AD=DC=2，AB=1．
（Ⅰ）求证：平面SAD⊥平面SCD；
（Ⅱ）求二面角S-BC-D的余弦值；
（Ⅲ）M为SC中点，在四边形ABCD所在的平面内是否存在一点N，使得MN⊥平面SBD，若存在，求三角形ADN的面积；若不存在，请说明理由．
求函数y=|x2-3x+2|的单调区间．
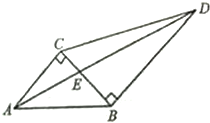如图，两块直角三角板拼在一起，已知∠ABC=45°，∠BCD=60°．
（1）若记
AB
=
a
，
AC
=
b
，试用
a
，
b
表示向量
AD
，
CD
；
（2）若AB=
2
，求
AE
•
CD
．
已知曲线C：y2=2x（y≥0），A1（x1，y1），A2（x2，y2），…An（xn，yn）…是曲线C上的点，且满足0＜x1＜x2＜…＜xn＜…，一列点Bi（ai，0）（i=1，2，…）在x轴上，且△Bi-1AiBi（B0是坐标原点）是以Ai为直角顶点的等腰直角三角形．
（Ⅰ）求A1、B1的坐标；
（Ⅱ）求数列{yn}的通项公式；
（Ⅲ）令bi=
1
a
，ci=
(
2
)-yi
2
，是否存在正整数N，当n≥N时，都有
n
i=1
bi＜
n
i=1
ci，若存在，求出N的最小值并证明；若不存在，说明理由．
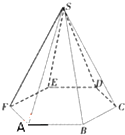正六棱锥的底面周长为24，侧面与底面所成角为60°．求：
（1）棱锥的高；
（2）侧棱长；
（3）侧棱与底面所成角的正切值．
已知数列{an}的前n项和Sn=-an-（
1
2
）n-1+2（n∈N*），数列{bn}满足bn=2nan．
（Ⅰ）求证数列{bn}是等差数列，并求数列{an}的通项公式；
（Ⅱ）设cn=log2
n
an
，数列{
2
cncn+2
}的前n项和为Tn，求满足Tn＜
25
21
（n∈N*）的n的最大值．
已知函数f（x）在其定义域（0，+∞）上是增函数，f（2）=1，f（xy）=f（x）+f（y）
（1）求f（8）的值；
（2）解不等式f（x）+f（x-2）≤3．
已知集合M={（x，y）|y=f（x）}，若对于任意实数（x1，y1）∈M，存在（x2，y2）∈M，使得x1x2+y1y2=0成立，则称集合M是“垂直对点集”，给出下列四个集合：
①M={（x，y）|y=-
1
x
}    ②M={（x，y）|y=x2-1}
③M={（x，y）|y=ex-2}   ④M={（x，y）|y=cosx}
其中是“垂直对点集”的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网