题目内容
6.如2x+2-x=5,求4x+$\frac{1}{{4}^{x}}$的值.分析 利用4x+$\frac{1}{{4}^{x}}$=(2x+2-x)2-2即可得出.
解答 解:∵2x+2-x=5,∴4x+$\frac{1}{{4}^{x}}$=(2x+2-x)2-2=23.
点评 本题考查了指数运算性质、乘法公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.矩形ABCD的对角线AC,BD成60°角,把矩形所在的平面以AC为折痕,折成一个直二面角D-AC-B,连接BD,则BD与平面ABC所成角的正切值为( )
| A. | $\sqrt{\frac{7}{10}}$ | B. | $\frac{\sqrt{21}}{7}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
18.已知函数f(x)=x3+ax2+(a+6)x+1有极值,则a的取值范围是( )
| A. | -1<a<2 | B. | -3<a<6 | C. | a<-3或a>6 | D. | a<-1或a>2 |
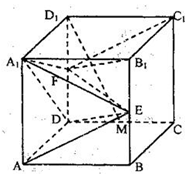 在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.
在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点. 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=4$\sqrt{3}$,M($\sqrt{3}$,-$\frac{\sqrt{13}}{2}$)是椭圆上一点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=4$\sqrt{3}$,M($\sqrt{3}$,-$\frac{\sqrt{13}}{2}$)是椭圆上一点.