题目内容
6. 三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC=2.
三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC=2.(1)求证:HI∥平面PAB;
(2)若AC⊥BC,求点C到平面FGH的距离.
分析 (1)利用中位线定理、面面线面平行的判定与性质定理即可证明.
(2)利用余弦定理可得cos∠GHF,根据VC-FGH=VF-CGH,即可得出.
解答 (1)证明:∵F,G,H,分别是PC,AC,BC的中点,
∴GH∥AB,FG∥PA.
∵GH?平面PAB,FG?平面PAB,
∴GH∥平面PAB,FG∥平面PAB.
∵FG∩GH=G,∴平面PAB∥平面FGH.
∵HI?平面FGH,∴HI∥平面ABD.
(2)解:由题意可得:HF=$\frac{\sqrt{5}}{2}$,HG=1,GF=$\frac{\sqrt{7}}{2}$.
故cos∠GHF=$\frac{1+\frac{5}{4}-\frac{7}{4}}{2×1×\frac{\sqrt{5}}{2}}$=$\frac{\sqrt{5}}{10}$,故sin∠GHF=$\frac{\sqrt{95}}{10}$,
记点C到平面FGH的距离为h,
∵VC-FGH=VF-CGH,
∴$\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×\frac{\sqrt{3}}{2}×1$=$\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{5}}{2}×\frac{\sqrt{95}}{2}$×h,
解得h=$\frac{\sqrt{57}}{19}$.
点评 本题考查了面面线面平行的判定与性质定理、三角形中位线定理、“等体积变形”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设F1和F2是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,若△F1PF2的面积是2,则b的值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
16.设f(x)是可导函数,且$\lim_{△x→0}\frac{{f({x_0})-f({{x_0}+2△x})}}{△x}=2$,则f'(x0)=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 0 | D. | -2 |
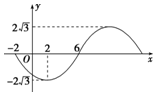 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.