题目内容
3.观察式子:1+$\frac{1}{{2}^{2}}$<$\frac{3}{2}$;1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$<$\frac{5}{3}$,1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$<$\frac{7}{4}$…则可归纳出第n-1个式子为1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$.分析 根据规律,左边是正整数n的平方的倒数和,右边是分子是正奇数,分母是正整数n,可以猜想结论.
解答 解:根据规律,左边是正整数n的平方的倒数和,右边是分子是正奇数,分母是正整数n,
可以猜想的结论为:当n∈N且n≥2时,恒有1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$.
故答案为:1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$<$\frac{2n-1}{n}$.
点评 本题考查的知识点是归纳推理其中分析已知中的式子,分析出两个式子之间的数据变化规律是解答的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
8.设a=x,b=sinx,c=tanx,0<x<$\frac{π}{2}$,则( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
8.函数$y=\frac{1}{x}$在x=1处的导数等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
12.已知集合A={x|x≥3或x≤-1},B={x|=-2≤x≤2},则A?B=( )
| A. | [-2,-1] | B. | [-1,2) | C. | [-1,1] | D. | [1,2) |
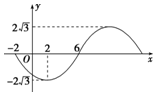 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.