题目内容
20.已知直线m,n和平面α满足m⊥α,m⊥n,则n与α的位置关系为( )| A. | n⊥α | B. | n?α | C. | n∥α或n?α | D. | 都有可能 |
分析 根据线面的位置关系进行分类讨论,分别利用线面垂直的性质进行说明即可.
解答 解:当n?α时,m⊥α,则m⊥n,
当n∥α时,m⊥α,则m⊥n,
故当m⊥α,m⊥n⇒n∥α或n?α
故选:C.
点评 本题主要考查了直线与平面垂直的性质,以及空间想象能力,推理能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
8.函数$y=\frac{1}{x}$在x=1处的导数等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
5.如果直线 l 经过两直线2x-3y+1=0和3x-y-2=0的交点,且与直线y=x垂直,则原点到直线 l 的距离是( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
12.已知集合A={x|x≥3或x≤-1},B={x|=-2≤x≤2},则A?B=( )
| A. | [-2,-1] | B. | [-1,2) | C. | [-1,1] | D. | [1,2) |
10.sin4cos3tan2的值为( )
| A. | 负数 | B. | 正数 | C. | 0 | D. | 不存在 |
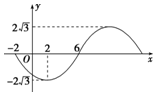 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示.