��Ŀ����
2����f��x���Ƕ��������������ϵĺ����������㣺���ڶ������������k����f��k����k2��������f��k+1���ݣ�k+1��2������������������ȷ���ǣ�������| A�� | ��f��3����9���������������k��N*������f��k����k2���� | |
| B�� | ��f��3����9���������������k��3��k��N*������f��k����k2���� | |
| C�� | ��f��3����9���������������k��3��k��N*������f��k����k2���� | |
| D�� | ��f��3��=9���������������k��3��k��N*������f��k����k2���� |
���� ����������Ϻ������������жϼ��ɣ�
��� �⣺A����f��3����9��������f��4����16��������f��k����k2��������k��3�������������жϵ�k=1��2ʱ�Ƿ��������A����
B����f��3����9��������f��4����16��������f��k����k2��������k��3����������B����
C����f��3����9��������f��4����16��������f��k����k2��������k��3����������C����
D����f��3��=9������f��3����9��������f��4����16��������f��k����k2��������k��3����������D��ȷ��
��ѡ��D
���� ������Ҫ�������������Ӧ�ã������������е����ǽ������Ĺؼ���

��ϰ��ϵ�д�
 ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
�����Ŀ
3����֪ʵ��x��y����$\left\{\begin{array}{l}x-2y-2��0\\ 2x+y-4��0\\ x-y-3��0\end{array}\right.$��x2+��y+2��2��ȡֵ��Χ�ǣ�������
| A�� | [$\frac{65}{9}$��25] | B�� | [$\frac{36}{5}$��25] | C�� | [16��25] | D�� | [9��25] |
10����O�İ뾶Ϊ1�������һСԲO1������A��B���������Ϊ$\frac{��}{3}$��OO1=$\frac{\sqrt{2}}{2}$�����AO1B=��������
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{2}$ | C�� | $\frac{2��}{3}$ | D�� | �� |
7��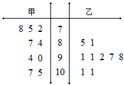 ij���˶���ס�����������˶�Ա�ɼ���ͼ��ʾ���ס��ҵ�ƽ�����ֱ�ΪΪ $\overline{{x}_{��}}$��$\overline{{x}_{��}}$������ֱ�Ϊs��2��s��2��������
ij���˶���ס�����������˶�Ա�ɼ���ͼ��ʾ���ס��ҵ�ƽ�����ֱ�ΪΪ $\overline{{x}_{��}}$��$\overline{{x}_{��}}$������ֱ�Ϊs��2��s��2��������
 ij���˶���ס�����������˶�Ա�ɼ���ͼ��ʾ���ס��ҵ�ƽ�����ֱ�ΪΪ $\overline{{x}_{��}}$��$\overline{{x}_{��}}$������ֱ�Ϊs��2��s��2��������
ij���˶���ס�����������˶�Ա�ɼ���ͼ��ʾ���ס��ҵ�ƽ�����ֱ�ΪΪ $\overline{{x}_{��}}$��$\overline{{x}_{��}}$������ֱ�Ϊs��2��s��2��������| A�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 | B�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 | ||
| C�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 | D�� | $\overline{{x}_{��}}$��$\overline{{x}_{��}}$��s��2��s��2 |
12��һƽ����뾶ΪR����O�İ뾶OA���е㣬�Ҵ�ֱ�ڸð뾶OA�����ƽ�����Ľ������Ϊ��������
| A�� | $\frac{1}{2}��{R^2}$ | B�� | $\frac{{\sqrt{3}}}{2}��{R^2}$ | C�� | ��R2 | D�� | $\frac{3}{4}��{R^2}$ |
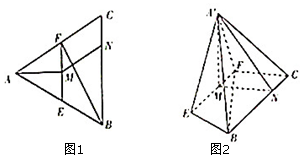 ��ͼ����֪�ȱߡ�ABC�У�E��F�ֱ�ΪAB��AC�ߵ��е㣬MΪEF���е㣬NΪBC����һ�㣬��CN=$\frac{1}{4}$BC������AEF��EF�۵���A'EF��λ�ã�ʹƽ��A'EF��ƽ��EFCB��
��ͼ����֪�ȱߡ�ABC�У�E��F�ֱ�ΪAB��AC�ߵ��е㣬MΪEF���е㣬NΪBC����һ�㣬��CN=$\frac{1}{4}$BC������AEF��EF�۵���A'EF��λ�ã�ʹƽ��A'EF��ƽ��EFCB��