题目内容
已知：圆C：x2+y2-8y+12=0，直线l：ax+y+2a=0．
（1）当a为何值时，直线l与圆C相切；
（2）当直线l与圆C相交于A、B两点，且AB=2时，求直线l的方程．
（1）当a为何值时，直线l与圆C相切；
（2）当直线l与圆C相交于A、B两点，且AB=2时，求直线l的方程．
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：（1）将圆C的方程配方得标准方程，确定圆心与半径，利用线l与圆C相切，则有
=2，即可求出a的值；
（2）确定圆心到直线的距离，可求a，即可求直线l的方程．
| |4+2a| | ||
|
（2）确定圆心到直线的距离，可求a，即可求直线l的方程．
解答：
解：将圆C的方程x2+y2-8y+12=0配方得标准方程为x2+（y-4）2=4，则此圆的圆心为（0，4），半径为2．
（1）若直线l与圆C相切，则有
=2，解得a=-
．…（5分）
（2）∵AB=2
∴圆心到直线的距离为
=
，
∴
=
，
解得a=-8±
．
故所求直线方程为（-8±
）x+y+2（-8±
）=0．…（12分）
（1）若直线l与圆C相切，则有
| |4+2a| | ||
|
| 3 |
| 4 |
（2）∵AB=2
∴圆心到直线的距离为
| 4-1 |
| 3 |
∴
| |4+2a| | ||
|
| 3 |
解得a=-8±
| 51 |
故所求直线方程为（-8±
| 51 |
| 51 |
点评：本题考查直线和圆的方程的应用，考查直线和圆的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知角θ的顶点与原点重合，始边与x轴的正半轴重合，终边过x=1与曲线y=2x的交点，则cos2θ=（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知集合A={x|x2-2x-8＜0}，B={y|y=log2（x2+2）}，则A∩B=（ ）
| A、（-2，-1] |
| B、[-1，4） |
| C、（-∞，4） |
| D、[1，4） |
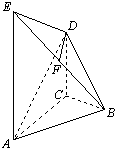在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．