题目内容

13．已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为$\frac{16π}{3}$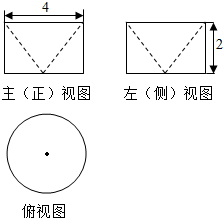

分析 几何体为圆柱挖去一个圆锥，根据三视图可得圆锥与圆柱的底面直径都为4，高都为2，把数据代入圆锥与圆柱的体积公式计算可得答案．

解答 解：由三视图知：几何体为圆柱挖去一个圆锥，且圆锥与圆柱的底面直径都为4，高为2，
∴几何体的体积V1=π×22×2-$\frac{1}{3}$×π×22×2=$\frac{16π}{3}$．
故答案为：$\frac{16π}{3}$．

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
3．已知x，y满足约束条件，$\left\{\begin{array}{l}{y≤1}\\{x+y-2≥0}\\{x-y-1≤0}\end{array}\right.$，则目标函数z=2x-y的最大值为（　　）
A．1B．3C．$\frac{5}{2}$D．$\frac{7}{2}$
4．设函数f（x）=sin（ωx+ϕ），（ω＞0，-π＜ϕ＜0）的两个相邻的对称中心分别为（$\frac{π}{8}$，0），$（\frac{5π}{8}，0）$
（1）求f（x）的解析式；
（2）求函数f（x）图象的对称轴方程；
（3）用五点法作出函数f（x）在[0，π]上的简图．
1．等比数列{an}前n项和为Sn=a+（$\frac{1}{3}$）n，n∈N*，则$\lim_{n→∞}$（a1+a3+a5+…+a2n-1）=-$\frac{3}{4}$．
8．给出下列四个命题：
①当x＞0且x≠1时，有lnx+$\frac{1}{lnx}$≥2；
②△ABC中，sinA＞sinB当且仅当A＞B；
③已知Sn是等差数列{an}的前n项和，若S7＞S5，则S9＞S3；
④函数y=f（1+x）与函数y=f（1-x）的图象关于直线x=1对称．
其中正确命题的序号为②③．
18．有4个命题：
（1）三点确定一个平面．
（2）梯形一定是平面图形．
（3）平行于同一条直线的两直线平行．
（4）垂直于同一直线的两直线互相平行．
其中正确命题的个数为（　　）
A．0B．1C．2D．3
5．△ABC中，已知3acosC=2ccosA，tanA=$\frac{1}{3}$，则B=$\frac{3π}{4}$．
2．设函数f（x）=cos（2x-$\frac{4π}{3}$）+2cos2x，
（Ⅰ）求f（x）的最大值，并写出使f（x）取最大值时x的集合；
（Ⅱ）已知△ABC中，角A、B、C的对边分别为a、b、c，若f（B+C）=$\frac{3}{2}$，b+c=2，a=1，求△ABC的面积的最大值．
3．已知直线y=x+1交椭圆${x^2}+\frac{y^2}{2}=1$于A、B两点，则弦AB的长为（　　）
A．$\frac{{\sqrt{2}}}{3}$B．$\frac{{2\sqrt{2}}}{3}$C．$\frac{{4\sqrt{2}}}{3}$D．$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网