题目内容
若a>b>0,则下列不等式成立的是( )
A、a>b>
| ||||
B、a>
| ||||
C、a>
| ||||
D、a>
|
考点:不等关系与不等式
专题:不等式的解法及应用
分析:利用不等式的性质、基本不等式的性质即可得出.
解答:
解:∵a>b>0,
∴a>
>
>b,
故选:D.
∴a>
| a+b |
| 2 |
| ab |
故选:D.
点评:本题考查了不等式的性质、基本不等式的性质,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知函数y=x2-2x+3在[0,a](a>0)上最大值是3,最小值是2,则实数a的范围是( )
| A、0<a<1 |
| B、0<a≤2 |
| C、1≤a≤2 |
| D、0≤a≤2 |
关于x的不等式(mx-1)(x-2)<0的解为2<x<
,则m的取值范围是( )
| 1 |
| m |
A、m<
| ||
| B、m>0 | ||
C、0<m<
| ||
| D、0<m<2 |
函数y=f(x)满足:
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
| A、f(-1)>f(2) |
| B、f(-1)<f(2) |
| C、f(-1)=f(2) |
| D、无法确定 |
“x(x-3)<0”是“|x-1|<2”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
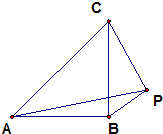 如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.
如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.