题目内容
在正方体ABCD﹣A1B1C1D1中,点M为棱AA1的中点,则直线BC1与平面MC1D1所成角的正弦值是( )
A. B.
B. C.
C. D.
D.
C
【解析】
试题分析:设正方体的边长为1,以D点为坐标原点,以DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,求出平面MC1D1的一个法向量为 ,然后求出法向量为
,然后求出法向量为 与
与 夹角的余弦值即为直线BC1与平面MC1D1所成角的正弦值.
夹角的余弦值即为直线BC1与平面MC1D1所成角的正弦值.
【解析】
设正方体的边长为1,以D点为坐标原点,以DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系
则M(1,0, ),D1(0,0,1),C1(0,1,1),B(1,1,0),
),D1(0,0,1),C1(0,1,1),B(1,1,0),
则 =(﹣1,0,
=(﹣1,0, ),
), =(﹣1,1,
=(﹣1,1, ),
), =(﹣1,0,1)
=(﹣1,0,1)
设平面MC1D1的一个法向量为 =(x,y,z)
=(x,y,z)
则 即
即
∴取x=1,则z=2即 =(1,0,2)
=(1,0,2)
设直线BC1与平面MC1D1所成角为θ,
则sinθ=|cosα|=| |=|
|=| |=
|=
故选C.


练习册系列答案
相关题目
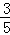 ,
, ),求cos2
),求cos2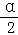 ﹣sin2
﹣sin2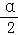 cos
cos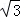 cosα的值域.
cosα的值域.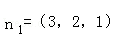 ,平面β的法向量为
,平面β的法向量为 ,则平面α与β夹角(锐角)的余弦是( )
,则平面α与β夹角(锐角)的余弦是( )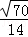 B.
B.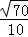 C.
C.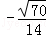 D.﹣
D.﹣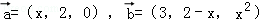 ,且
,且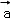 与
与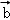 的夹角为钝角,则x的取值范围是( )
的夹角为钝角,则x的取值范围是( )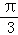 <∠PAC<
<∠PAC<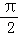
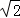
 的坐标为( )
的坐标为( )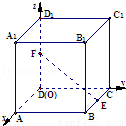
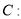
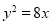 ,过点
,过点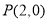 的直线与抛物线交于
的直线与抛物线交于 ,
,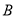 两点,
两点,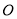 为坐标原点,则
为坐标原点,则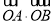 的值为
的值为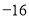 (B)
(B)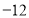 (C)
(C)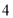 (D)
(D)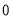
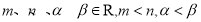 ,若
,若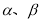 是函数
是函数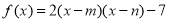 的零点,则
的零点,则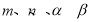 四个数按从小到大的顺序是 (用符号
四个数按从小到大的顺序是 (用符号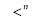 连接起来).
连接起来).