题目内容
已知抛物线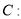
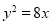 ,过点
,过点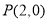 的直线与抛物线交于
的直线与抛物线交于 ,
,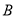 两点,
两点, 为坐标原点,则
为坐标原点,则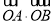 的值为
的值为
(A)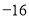 (B)
(B)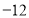 (C)
(C)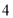 (D)
(D)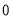
B
【解析】当直线斜率不存在时,方程为x=2,于是A(2,4),B(2,-4), =2×2+(-4)×(-4)=-12
=2×2+(-4)×(-4)=-12
已经可以排除A、C、D,选B
当斜率存在时,设直线方程为y=k(x-2),代入抛物线方程
于是k2(x-2)2=8x
整理得:k2x2-(4k2+8)x+4k2=0
记A(x1,y1),B(x2,y2),则
 =x1x2+y1y2=x1x2+k2[x1x2-2(x1+x2)+4]
=x1x2+y1y2=x1x2+k2[x1x2-2(x1+x2)+4]
=(1+k2)x1x2-2k2(x1+x2)+4k2
=
=-12.选B
考点:直线与抛物线的位置关系,抛物线的标准方程,平面向量

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a>0,且a≠1),f′(x)g(x)<f(x)g′(x),
(a>0,且a≠1),f′(x)g(x)<f(x)g′(x), ,则a的值为( )
,则a的值为( ) C.
C. D.
D.
 B.
B. C.
C. D.
D.
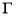 :
: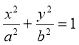 (
( )的右焦点为
)的右焦点为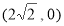 ,且过点
,且过点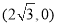 .
. 与椭圆
与椭圆 交于不同两点
交于不同两点 、
、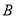 ,且
,且 .若点
.若点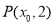 满足
满足 ,求
,求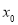 的值.
的值. 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, .则边
.则边 的长度为__________..
的长度为__________..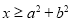 ,则
,则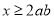 ”的逆命题是
”的逆命题是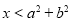 ,则
,则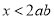
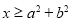 ,则
,则 为正三角形,
为正三角形, 平面
平面 ,
, ,
, 为
为 的中点,
的中点, ,
, .
.

 平面
平面 ;
; 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. ,点
,点 点
点 与点
与点 关于直线
关于直线 对称,且
对称,且 .直线
.直线 是过点
是过点 的任意一条直线.
的任意一条直线. 所在曲线
所在曲线 的轨迹方程;
的轨迹方程; 两点,且
两点,且 ,求直线
,求直线 两点,求以
两点,求以 的长为直径且经过坐标原点
的长为直径且经过坐标原点 的圆的方程.
的圆的方程. 的顶点在坐标原点,焦点与双曲线:
的顶点在坐标原点,焦点与双曲线: 的右焦点重合,则抛物线
的右焦点重合,则抛物线