题目内容
7.已知函数f(x)=sinxcosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$.(1)求函数f(x)的周期;
(2)求函数f(x)在[-$\frac{π}{6}$,$\frac{2π}{3}$]的取值范围.
分析 (1)化简函数f(x)为Asin(ωx+φ)的形式,求出最小正周期;
(2)由x∈[-$\frac{π}{6}$,$\frac{2π}{3}$]求出相位的取值范围,再计算f(x)的取值范围即可.
解答 解:(1)函数f(x)=sinxcosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$sin2x-$\sqrt{3}×$$\frac{cos2x+1}{2}$+$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x
=sin(2x-$\frac{π}{3}$),…(4分)
由T=$\frac{2π}{2}$得,最小正周期T=π;…(6分)
(2)∵x∈[-$\frac{π}{6}$,$\frac{2π}{3}$],∴-$\frac{2π}{3}$≤2x-$\frac{π}{3}$≤π,…(7分)
∴-1≤sin(2x-$\frac{π}{3}$)≤1,…(9分)
函数f(x)在[-$\frac{π}{6}$,$\frac{2π}{3}$]的取值范围:[-1,1].
点评 本题考查了三角函数的化简与形如f(x)=Asin(ωx+φ)+b的图象与性质的应用问题,是基础题目.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
17.已知集合M={x|y=ln(1-x)},集合N={y|y=3x,x∈R},则M∩N=( )
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
18.设集合A={x|(x-1)(x-2)2=0},则集合A中元素的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.函数f(x)=x3-3x在[-3,$\frac{3}{2}$]上的最大值和最小值分别是( )
| A. | 2,-2 | B. | 2,-18 | C. | 18,-2 | D. | 18,-18 |
12.设a=log54,b=log0.55,c=log45,则( )
| A. | a<c<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
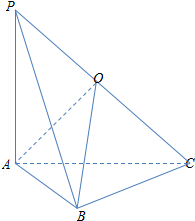 如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,且AB=BC=1,PA=$\sqrt{2}$,O为线段PC的中点,
如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,且AB=BC=1,PA=$\sqrt{2}$,O为线段PC的中点,