题目内容
17.设a>0,解关于x的不等式:2a(1-a)x2-2(1-a)x+1>0.分析 根据判别式,再对参数a的取值范围进行讨论,从而求出不等式的解集.
解答 解:2a(1-a)x2-2(1-a)x+1>0,△=4(1-a)2-8a(1-a)=4(1-a)(1-3a),
当△<0时,即$\frac{1}{3}$<a<1时,此时2a(1-a)>0,不等式对任意x恒成立,故不等式的解集为R,
当△≥0时,即a≤$\frac{1}{3}$或a≥1时,
①当0<a≤$\frac{1}{3}$时,此时2a(1-a)>0,解不等式得x<$\frac{1-a-\sqrt{(1-a)(1-3a)}}{2a(1-a)}$或x>$\frac{1-a+\sqrt{(1-a)(1-3a)}}{2a(1-a)}$,
此时不等式的解集为(-∞,$\frac{1-a-\sqrt{(1-a)(1-3a)}}{2a(1-a)}$)∪($\frac{1-a+\sqrt{(1-a)(1-3a)}}{2a(1-a)}$,+∞);
②当a=1时,不等式等价于1>0,不等式对任意x恒成立,故不等式的解集为R,
③当a>1时,此2a(1-a)<0,解不等式得x<$\frac{1-a-\sqrt{(1-a)(1-3a)}}{2a(1-a)}$<x<$\frac{1-a+\sqrt{(1-a)(1-3a)}}{2a(1-a)}$,
此时不等式的解集为($\frac{1-a-\sqrt{(1-a)(1-3a)}}{2a(1-a)}$,$\frac{1-a+\sqrt{(1-a)(1-3a)}}{2a(1-a)}$).
综上所述:当0<a≤$\frac{1}{3}$时,不等式的解集为(-∞,$\frac{1-a-\sqrt{(1-a)(1-3a)}}{2a(1-a)}$)∪($\frac{1-a+\sqrt{(1-a)(1-3a)}}{2a(1-a)}$,+∞),
当$\frac{1}{3}$<a≤1时,不等式的解集为R,
当a>1时,不等式的解集为($\frac{1-a-\sqrt{(1-a)(1-3a)}}{2a(1-a)}$,$\frac{1-a+\sqrt{(1-a)(1-3a)}}{2a(1-a)}$).
点评 本题考查了含有字母系数的一元二次不等式的解法与应用问题,解题时应用分类讨论的数学思想,是综合题目.

| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰三角或直角三角形 |
| A. | -2n | B. | (-2)n | C. | -4n | D. | (-4)n |
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
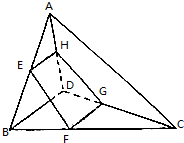 已知空间四边形ABCD,E、H分别是AB、AD的点,F、G分别是边BC、DC的点(如图),且EFGH是矩形,求证:
已知空间四边形ABCD,E、H分别是AB、AD的点,F、G分别是边BC、DC的点(如图),且EFGH是矩形,求证: