题目内容
已知抛物线y2=4x,过点P(-1,0)作直线l交抛物线于A、B两点,若以AB为直径的圆经过抛物线的焦点F,求l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:设l的方程为:y=k(x+1),联立
,得k2x2+(2k2-4)x+k2=0,由此利用韦达定理、弦长公式和点到直线的距离公式能求出直线方程.
|
解答:
解:抛物线y2=4x的焦点F(1,0),
直线l过(-1,0),设l的方程为:y=k(x+1),
联立
,得k2x2+(2k2-4)x+k2=0,
∵直线l交抛物线于A、B两点,
∴△>0,设A(x1,y1),B(x2,y2),
则x1+x2=-
,x1x2=1,
y1+y2=k(x1+1)+k(x2+1)=-
+2k=
,
∴以AB为直径的圆的圆心坐标为M(-
,
),
|MF|=
=
,
|AB|=
•
,
∵以AB为直径的圆经过抛物线的焦点F,
∴
•
=
,
解得k2=
,即k=±
,
∴直线l的方程为y=±
(x+1).
直线l过(-1,0),设l的方程为:y=k(x+1),
联立
|
∵直线l交抛物线于A、B两点,
∴△>0,设A(x1,y1),B(x2,y2),
则x1+x2=-
| 2k2-4 |
| k2 |
y1+y2=k(x1+1)+k(x2+1)=-
| 2k2-4 |
| k |
| 4 |
| k |
∴以AB为直径的圆的圆心坐标为M(-
| k2-2 |
| k2 |
| 2 |
| k |
|MF|=
(1+
|
| ||
| k2 |
|AB|=
| 1+k2 |
(-
|
∵以AB为直径的圆经过抛物线的焦点F,
∴
| 1 |
| 2 |
| 1+k2 |
(-
|
| ||
| k2 |
解得k2=
| 3 |
| 4 |
| ||
| 2 |
∴直线l的方程为y=±
| ||
| 2 |
点评:本题考查直线方程的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
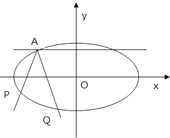 如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).
如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).