题目内容
18. 已知函数f(x)=1+$\frac{x-|x|}{4}$.
已知函数f(x)=1+$\frac{x-|x|}{4}$.(1)用分段函数的形式表示函数f(x);
(2)在平面直角坐标系中画出函数f(x)的图象;
在同一平面直角坐标系中,再画出函数g(x)=$\frac{1}{x}$(x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)>g(x)的解集.
分析 (1)已知函数f(x)=1+$\frac{x-|x|}{4}$.,首先要去掉绝对值,讨论x与0的关系,从而进行求解;
(2)根据f(x)的解析式,可以画出f(x)的图象;再画出g(x)的图象,可以直接看出不等式的解集;
解答 解:解:(Ⅰ)因为当x≥0时,f(x)=1;
当x<0时,f(x)=$\frac{1}{2}$x+1;
所以$f(x)=\left\{{\begin{array}{l}{1,x≥0}\\{\frac{1}{2}x+1,x<0}\end{array}}\right.$;
(2)函数图象如图: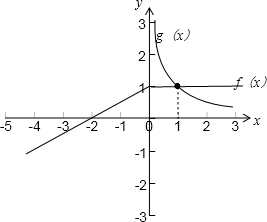
由上图可知当x>1时,f(x)>g(x),
∴不等式f(x)>$\frac{1}{x}$的解集为{x|x>1}
点评 此题主要考查分段函数的性质,以及数形结合的方法求解不等式的解集问题,是一道基础题;

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
9.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$(λ,μ∈R),若M为线段AB的中点,并且|$\overrightarrow{MC}$|=1,则λ+μ的最大值为( )
| A. | 1+$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 1 |
7.在等差数列{an}中,已知a1=3,a9=11则前9项和S9=( )
| A. | 63 | B. | 65 | C. | 72 | D. | 62 |
8.函数f(x)=$\frac{ln(-{x}^{2}+2x+3)}{\sqrt{1-x}}$+x0的定义域为( )
| A. | (-1,1) | B. | (-1,1) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(0,3) |
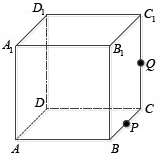 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是①③④⑤(写出所有正确命题的编号).