Question

17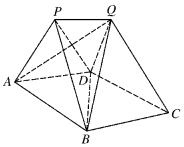．如图，P-ABD和Q-BCD为两个全等的正棱锥，且A，B，C，D四点共面，其中AB=1，∠APB=90°．
（Ⅰ）求证：BD⊥平面APQ；
（Ⅱ）求直线PB与平面PDQ所成角的正弦值．

Answer 1

分析 （Ⅰ）由题意分别过P、Q作PE⊥平面ABD，QF⊥平面BCD，可得E、F分别为底面正三角形ABD与BCD的中心．连接EF交BD于G，可得PG⊥BD，QG⊥BD，由线面垂直的判定及性质可得BD⊥PQ，再由正三棱锥的性质可得PA⊥BD，则BD⊥平面APQ；
（Ⅱ）由已知求得PQ，PE的长，求得四面体B-PQD的体积，利用等积法求出B到平面PQD的距离，则直线PB与平面PDQ所成角的正弦值可求．

解答 （Ⅰ）证明：由P-ABD，Q-BCD是相同正三棱锥，且∠APB=90°，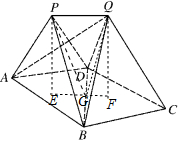
分别过P、Q作PE⊥平面ABD，QF⊥平面BCD，垂足分别为E、F，
则E、F分别为底面正三角形ABD与BCD的中心．
连接EF交BD于G，则G为BD的中点，连接PG、QG，则PG⊥BD，QG⊥BD，
又PG∩QG=G，∴BD⊥平面PQG，则BD⊥PQ，
再由正三棱锥的性质可得PA⊥BD，
又PQ∩PA=P，∴BD⊥平面APQ；
（Ⅱ）∵正三棱锥的底面边长为1，且∠APB=90°，
∴PQ=EF=2EG=2×$\frac{1}{3}$AG=2×$\frac{1}{3}×$$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$，
PE=$\sqrt{（\frac{\sqrt{2}}{2}）^{2}-（\frac{\sqrt{3}}{3}）^{2}}=\frac{\sqrt{6}}{6}$，
则${V}_{B-PQD}=\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}}{3}×\frac{\sqrt{6}}{6}×1=\frac{\sqrt{2}}{36}$．
△PDQ底边PQ上的高为$\sqrt{（\frac{\sqrt{2}}{2}）^{2}-（\frac{\sqrt{3}}{6}）^{2}}=\frac{\sqrt{15}}{6}$，
∴${S}_{△PDQ}=\frac{1}{2}×\frac{\sqrt{3}}{3}×\frac{\sqrt{15}}{6}=\frac{\sqrt{5}}{12}$．
设B到平面PQD的距离为h，则$\frac{1}{3}×\frac{\sqrt{5}}{12}h=\frac{\sqrt{2}}{36}$，得h=$\frac{\sqrt{10}}{5}$．
∴直线PB与平面PDQ所成角的正弦值为$\frac{\frac{\sqrt{10}}{5}}{\frac{\sqrt{2}}{2}}=\frac{2\sqrt{5}}{5}$．

点评 本题考查直线与平面所成的角，考查线面垂直的判定，考查空间想象能力和思维能力，训练了利用等积法求多面体的体积，是中档题．