题目内容
9.($\frac{\sqrt{x}}{2}$+$\frac{2}{\root{3}{x}}$)10的展开式中常数项等于840,有理项有2项.分析 利用通项公式即可得出.
解答 解:($\frac{\sqrt{x}}{2}$+$\frac{2}{\root{3}{x}}$)10的展开式中通项公式:Tr+1=${∁}_{10}^{r}$$(\frac{\sqrt{x}}{2})^{10-r}$$(\frac{2}{\root{3}{x}})^{r}$=22r-10${∁}_{10}^{r}$${x}^{5-\frac{5r}{6}}$.
令$5-\frac{5r}{6}$=0,解得r=6,可得常数项=${2}^{2}{∁}_{10}^{6}$=840.
令$5-\frac{5r}{6}$=0,1,…5,
解得r=6,$\frac{24}{5}$,$\frac{18}{5}$,$\frac{12}{5}$,$\frac{6}{5}$,0.
可得有理项:${2}^{2}{∁}_{10}^{6}$,2-10x5.
故答案为:840,2.
点评 本题考查了二项式定理的通项公式、分类讨论方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
11.△ABC的内角A,B,C的对边分别是a,b,c,若a2=(b+c)2-4,△ABC的面积为$\sqrt{3}$,则A等于( )
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
4.方程(x+y-3)$\sqrt{{y}^{2}-4x}$=0表示的曲线是( )
| A. | 两条射线 | B. | 抛物线和一条线段 | ||
| C. | 抛物线和一条直线 | D. | 抛物线和两条射线 |
1.已知集合M={x|y=ln(2-x)},N={x|x2-3x-4≤0},则M∩N=( )
| A. | [-1,2) | B. | [-1,2] | C. | [-4,1] | D. | [-1,4] |
18.已知函数f(x)=2sin(ωx+φ)-1(ω>0,|φ|<π)的一个零点是$\frac{π}{3}$,函数y=f(x)图象的一条对称轴是x=-$\frac{π}{6}$,则ω取得最小值时,函数f(x)的单调区间是( )
| A. | [3kπ-$\frac{π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | B. | [3kπ-$\frac{5π}{3}$,3kπ-$\frac{π}{6}$],k∈Z | ||
| C. | [2kπ-$\frac{2π}{3}$,2kπ-$\frac{π}{6}$],k∈Z | D. | [2kπ-$\frac{π}{3}$,2kπ-$\frac{π}{6}$],k∈Z |
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.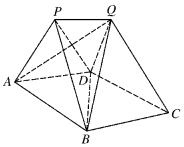 如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.
如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.