题目内容
5.(x+$\frac{1}{x}$-2)3展开式中的常数项为( )| A. | -8 | B. | -12 | C. | -20 | D. | 20 |
分析 利用通项公式即可得出.
解答 解:(x+$\frac{1}{x}$-2)3展开式中的通项公式:Tr+1=${∁}_{3}^{r}$(-2)3-r$(x+\frac{1}{x})^{r}$.
$(x+\frac{1}{x})^{r}$的通项公式:Tk+1=${∁}_{r}^{k}$${x}^{r-k}(\frac{1}{x})^{k}$=${∁}_{r}^{k}$xr-2k.
令r-2k=0,可得:k=0=r,k=1,r=2.
∴常数项=(-2)3+${∁}_{2}^{1}$×${∁}_{3}^{2}$×(-2)=-20.
故选:C.
点评 本题考查了二项式定理的通项公式、分类讨论方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
10.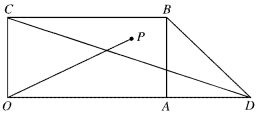 如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
 如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 3 |
15.已知命题p:若a,b是实数,则a>b是a2>b2的充分不必要条件;命题q:“?x∈R,x2+2>3x”的否定是“?x∈R,x2+2<3x”,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.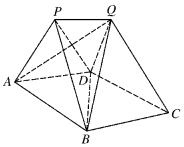 如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.
如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.