题目内容
在以O为极点的极坐标系中,直线l与曲线C的极坐标方程分别是ρcos(θ+
)=3
和ρsin2θ=8cosθ,已知直线l与曲线C交于点A、B,则线段AB的长为 .
| π |
| 4 |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,利用点到直线的距离公式求出弦心距,再利用弦长公式求出弦长.
解答:
解:直线l的极坐标方程是ρcos(θ+
)=3
,即
ρcosθ-
ρsinθ=3
,
化为直角坐标方程为 x-y-6=0.
曲线C的极坐标方程ρsin2θ=8cosθ,即ρ2sin2θ=8ρcosθ,即y2=8x.
由
,可得x2-20x+36=0,∴x1+x2=20,x1•x2=36,
弦长为
|x1-x2|=
•
=
•
=16
,
故答案为:16
.
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
化为直角坐标方程为 x-y-6=0.
曲线C的极坐标方程ρsin2θ=8cosθ,即ρ2sin2θ=8ρcosθ,即y2=8x.
由
|
弦长为
| 1+k2 |
| 1+1 |
| (x1+x2)2-4•x1•x2 |
| 2 |
| 400-144 |
| 2 |
故答案为:16
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式、弦长公式的应用,直线和圆的位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
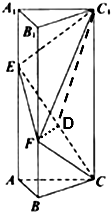 如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3
如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3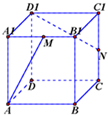 如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角
如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角